आकृति में, AD, माध्यिका है और DE || AB है। सिद्ध कीजिए कि BE माध्यिका है ।
Step by step video & image solution for आकृति में, AD, माध्यिका है और DE || AB है। सिद्ध कीजिए कि BE माध्यिका है । by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- चतुर्भुज BOOK - MBD HINDI-HARYANA BOARDCHAPTER - चतुर्भुज EXERCISE - महत्त्वपुर्ण उदाहरण (दीर्घ उत्तरात्मक प्रश्न)
1 Videos
- चतुर्भुज BOOK - MBD HINDI-HARYANA BOARDCHAPTER - चतुर्भुज EXERCISE - पाठ्य-पुस्तक प्रश्नावली 8.1
8 Videos
- आदर्श प्रश्न पत्र -3BOOK - MBD HINDI-HARYANA BOARDCHAPTER - आदर्श प्रश्न पत्र -3EXERCISE - खण्ड-द
6 Videos
- त्रिभुजBOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - दीर्घ उत्तरीय प्रश्न
1 Videos
Similar Questions
सिद्ध कीजिए कि एक वर्ग की क्रमागत भुजाओं के मध्य-बिंदुओं को मिलाकर बनाया गया चतुर्भुज भी वर्ग होता है।
View Solutionएक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
View Solutionयदि दो रेखाएं परस्पर प्रतिच्छेद करें , तो शीर्षाभिमुख कोण सामान होते हैं।
View Solutionकिसी Δ की समान भुजाओं के सम्मुख कोण समान होते हैं।
दिया है: ΔABC में AB=AC
सिद्ध करना है ∠C=∠B
View Solutionसिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय संख्याएँ है-
32√5
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionआकृति के अनुसार आकृति में PQ और XY समानान्तर रेखाएं है। ∠QRT=30∘ हो तो ∠TSY ज्ञात कीजिए।
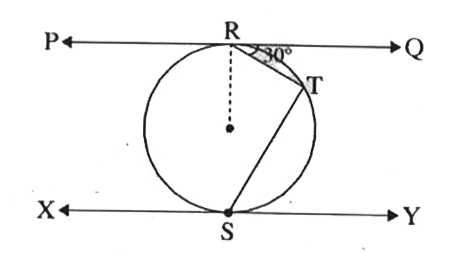
View Solutionसिद्ध कीजिए कि किसी गुणोत्तर श्रेढ़ी के आरम्भ और अंत से संदुररस्थ पदों का गुणनफलन सदैव अचर रहता है ।
View Solutionकिसी त्रिभुज एब्स के शीर्ष A(−3,4),B(6,−2) और C(2,5) है। बिन्दु A से होकर जाने वाली माध्यिका का समीकरण ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
View Solutionसिद्ध कीजिए कि f(x)=ax,o<a<1,R में ह्रासमान है।
View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में वर्धमान है ।
f(x)=logsinx,x∈(0,π2)
View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में ह्रासमान है ।
f(x)=−tan−1x,x∈R
View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में ह्रासमान है ।
f(x)=x2−2x+3,x<1
View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए हुए अन्तराल में ह्रासमान है -
f(x)=x2−2x+3,x<1
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solution
