बायो-सावर्ट नियम क्या है ? इसकी सहायता से वृत्ताकार धारावाही कुंडली की अक्षीय रेखा के किसी बिंदु पर चुम्बकीय क्षेत्र का सूत्र स्थापित कीजिए।
Video Solution
Text Solution
बायो - सावर्ट नियम - (विस्तृत उत्तरीय प्रश्न 1 देखें)
वृत्ताकार धारावाही कुण्डली की अक्षीय रेखा पर चुम्बकीय क्षेत्र - माना R त्रिज्या की एक वृत्ताकार कुण्डली में I धारा प्रवाहित हो रही है तथा कुण्डली की अक्ष पर केन्द्र O से x दूरी पर स्थित बिन्दु P पर चुम्बकीय क्षेत्र ज्ञात करना है
माना कुण्डली के शीर्ष पर कागज़ के तल के लम्बवत तथा बाहर की ओर दिष्ट एक धारावाही अल्पांश d→l है। इस अल्पांश के सापेक्ष बिन्दु P का स्थित सदिश →r है। बायो - सावर्ट के नियम से धारावाही अल्पांश के कारण बिन्दु P पर चुम्बकीय क्षेत्र
d→B=μ04π⋅Idlsin90∘r2=μ04πIdlr2
d→B को दो लम्बवत घटको में वियोजित करने पर घटक dBsinϕ कुण्डली की अक्ष से अनुदिश व घटक dBcosϕ, अक्ष के लम्बवत है।
कुण्डली के शीर्ष पर अल्पांश dl के ठीक विपरीत अल्पांश d→l लेते है इस अल्पांश के कारण बिन्दु P पर उत्पन्न चुम्बकीय d→B परिमाण में dB के बराबर होगा। इसे भी लम्बवत घटको में वियोजित करने पर घटक dBcosϕ घटक dBcosϕ को निरस्त कर देता है तथा घटक dBsinϕ कुण्डली की अक्ष के अनुदिश है।
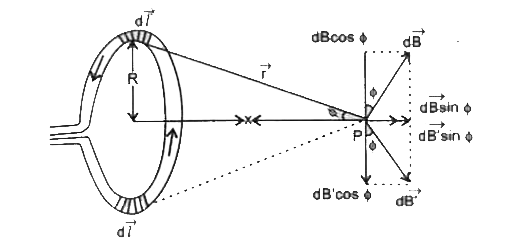
∴ पूरे लूप के कारण बिन्दु P पर चुम्बकीय क्षेत्र,
B=∫dBsinϕ=∫μ04πIdlr2×Rr
=μ04πIRr3∫dl=μ04πIR(√R2+x2)3×2πR
B=μ0IR22(R2+x2)3/2
यदि कुण्डली में फेरों की संख्या N हो तब,
B=μ0NIR22(R2+x2)3/2
|
Similar Questions
बायो सावर्ट का नियम
View Solutionएकसमान चुम्बकीय क्षेत्र में धारावाही कुंडली पर बल आघूर्ण
View Solutionबायो सावर्ट का नियम
View Solutionबायो सावर्ट का नियम
View Solutionबायो सावर्ट का नियम के अनुप्रयोग
View Solutionबायो सावर्ट का नियम के अनुप्रयोग
View Solutionवृत्ताकार धारावाही कुंडली के अक्ष पर एक बिंदु पर चुंबकीय क्षेत्र
View Solutionधारा का चुम्बकीय प्रभाव #!#ओर्स्टेड का प्रयोग #!#एम्पीयर के तैरने का नियम#!#विधुत धारावाही तार चालक का चुम्बकीय क्षेत्र #!#दाये हाथ का नियम #!#दाये हाथ की हथेली का नियम #!#बायो सेवर्ट का नियम
View Solution
