वृत्ताकार धारावाही कुण्डली अथवा लूप की अक्ष के अनुदिश चुम्बकीय क्षेत्र का व्यंजक स्थापित कीजिए।
Video Solution
Text Solution
वृत्ताकार धारावाही कुण्डली अथवा लूप की अक्ष के अनुदिश चुम्बकीय क्षेत्र - माना r त्रिज्या की एक वृत्ताकार कुण्डली में i धारा प्रवाहित हो रही है माना कुण्डली की अक्ष पर कुण्डली के केन्द्र O से x दूरी पर एक बिन्दु P है जहाँ पर चुम्बकीय क्षेत्र की तीव्रता ज्ञात करनी है (चित्र)। माना कुण्डली अनेक
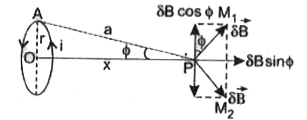
छोटे - छोटे अवयवों से मिलकर बना है इनमे से एक छोटा अवयव A है जो कागज़ के तल के लम्बवत है माना इस अवयव की लम्बाई δl है माना बिन्दु P से इस अवयव A की दूरी a है अतः बायो - सावर्ट के नियम से, बिन्दु P पर चुंबकीय क्षेत्र की तीव्रता
δB=μ04π<alsinθa2
परन्तु δl तथा r के बीच कोण θ=90∘ है अतः
δB=μ14π<ala2 (PM1 दिशा में)
धारा अवयव <al तथा a के बीच कोण θ=90∘ है अतः
δB=μ04π<ala2 (PM1 दिशा में)
चुम्बकीय क्षेत्र δB को अक्ष के अनुदिश व लम्बवत घटको में वियोजित करने पर, लम्बत घटक δBcosϕ परस्पर निरस्त हो जाएंगे जबकि अनुदिश घटक δBsinϕ जुड़ जाएंगे। अतः इनका परिमाण
B∮dBsinϕ परन्तु चित्र से, sinϕ=ra
अतः B=∮μ04πidla2×ra=μ04πira3∮dl
परन्तु कुण्डली की लम्बाई =∮dl=2πr तथा a=(r2+x2)1/2
अतः B=μ04π−2πir2(r2+x2)3/2=μ0ir22(r2+x2)3/2
यदि कुण्डली में N फेरे हो तो B=μ0Nir22(r2+x2)3/2
चुम्बकीय क्षेत्र B की दिशा कुण्डली की अक्ष के अनुदिश होगी। कुण्डली के केन्द्र पर x=0 है अतः कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र
B=μ0Ni2r
|
Similar Questions
आंकीक प्रश्न |विद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionधारावाही वृत्ताकार लूप और कुंडली के अक्ष पर चुंबकीय क्षेत्र
View SolutionRecap|धारावाही लूप के कारण चुम्ब्कीय क्षेत्र
View Solutionधारावाही चालक तार के कारण चुम्बकीय क्षेत्र
View Solutionवृत्ताकार धारावाही कुंडली के अक्ष पर एक बिंदु पर चुंबकीय क्षेत्र
View Solutionधारावाही लूप के कारण चुम्बकीय क्षेत्र
View Solutionसीधे धारावाही तार के कारण चुम्बकीय क्षेत्र
View Solutionधारावही लूप के कारण चुम्बकीय क्षेत्र
View Solution
