दो घर्षणरहित आनत पथ, जिनमे से एक ही ढाल अधिक है और दूसरे की ढाल कम है, बिंदु A पर मिलते है। बिंदु A से प्रत्येक पथ पर एक - एक पत्थर को विरामावस्था से नीचे सरकाया जाता है (चित्र)। क्या ये पत्थर एक ही समय पर नीचे पहुंचेगे ? क्या वे वहाँ एक ही चल से पहुंचगे ? व्याख्या कीजिए। यदि और h = 10 m दिया है तो दोनों पत्थरो की चल एवं उनके द्वारा नीचे पहुंचने में लिए गए समय क्या है ?
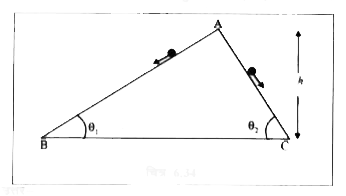
माना कि पत्थर 1 में उत्पन्न त्वरण है तब
यदि पत्थर 1 आनत तल AB पर फिसलने में समय लेता है ,
तब
[ ]
[ ]
. . . (1)
इसी प्रकार पत्थर 2 के लिए
. . . (2)
दोनों पत्थरो के लिए समान है।
समी (1) व (2) से
इसी प्रकार पत्थर 2 धरातल पर पत्थर 1 कि तुलना में पहले पहुंचेगा अब क्योकि दोनों पत्थर प्रारंभ में समान ऊंचाई h से फिसलते है। अतः
बिन्दु A पर स्थितिज ऊर्जा = बिन्दु B अथवा C पर गतिज ऊर्जा
. . . (3)
अतः दोनों पत्थर धरातल पर एक ही चल से पहुंचेगे
दिया गया है - मी.
समी. (1) से
= 2 . 86 सेकण्ड
समी. (2) से
सेकण्ड
समी. (3) से
मी. / से
Topper's Solved these Questions
- कार्य, ऊर्जा एवं शक्ति BOOK - SCIENCE PUBLICATIONCHAPTER - कार्य, ऊर्जा एवं शक्ति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (लघुत्तरात्मक प्रश्न)
9 Videos
- कार्य, ऊर्जा एवं शक्ति BOOK - SCIENCE PUBLICATIONCHAPTER - कार्य, ऊर्जा एवं शक्ति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (निबन्धात्मक प्रश्न )
4 Videos
- कार्य, ऊर्जा एवं शक्ति BOOK - SCIENCE PUBLICATIONCHAPTER - कार्य, ऊर्जा एवं शक्ति EXERCISE - NCERT (Text book problems)
23 Videos
- कणों के निकाय तथा घूर्णी गति BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न )
33 Videos
- गति के नियम BOOK - SCIENCE PUBLICATIONCHAPTER - गति के नियम EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न )
38 Videos
Similar Questions
एक मनुष्य नदी के बहाव के विरुद्ध नाव इस प्रकार चला रहा है कि किनारे के आपेक्ष नाव स्थित रहती है। क्या मनुष्य द्वारा लगाये गये बल के द्वारा कोई कार्य किया जा रहा है ?
View Solutionकार्य किसी कहते है ? परिवर्ती बल द्वारा किया गया कार्य किस प्रकार ज्ञात करेंगे ? उदाहरण सहित समझाइये।
View Solutionकिसी वस्तु पर किसी बल द्वारा किये गए कार्य का चिह्न समझना महत्वपूर्ण है। सावधानीपूर्वक बताइये की निम्नलिखित राशिया धनात्मक है या ऋणात्मक :
(a) किसी व्यक्ति द्वारा किसी कुएं में से रस्सी से बंधी बाल्टी को रस्सी द्वारा बाहर निकलने में किया गया कार्य |
(b) उपयुक्त स्थिति में गुरुत्वीय बल द्वारा किया गया कार्य |
(c) किसी आनत तल फिसलती हुई किसी वस्तु पर घर्षण द्वारा किया गया कार्य ।
(d) किसी खुरदरे क्षैतिज तल एकसमान वेग से गतिमान किसी वस्तु और लगाए गए बल द्वारा किया गया कार्य
(e) किसी दोलायमान लोलक को विरामावस्था में लाने के लिए वायु के प्रतिरोधी बल द्वारा किया गया कार्य |
View Solutionदो कण जिनके द्रव्यमान क्रमशः 100 ग्राम व 400 ग्राम है इनके स्थिति सदिश क्रमशः (2ˆi+4ˆj+2ˆk)सेमी. तथा (−6ˆi+3ˆj+2ˆk)सेमी. है। इनके द्रव्यमान केन्द्र का स्थिति सदिश ज्ञात कीजिए।
View Solution0.2 किग्रा. द्रव्यमान की क्रिकेट गेंद 20 मी./से. के वेग से गतिमान है। जिसे 0.4 सेकण्ड में विरामावस्था में लाया जाता है औसत बल की गणना कीजिए।
View Solutionएक अनभिनत पासे को 5 बार उछाला जाता है एक समसंख्या प्राप्त करना एक सफलता है तो प्रायिकता ज्ञात कीजिए - अधिक से अधिक 4 सफलताओ के लिए
View Solutionदो पासो को एक साथ चार बार फेका जाता है दोनों पासो पर प्राप्त अंको का योग 7 कम से कम दो बार आने की प्रायिकता ज्ञात कीजिए
View Solutionएक ही कोटि की दो वर्ग आव्यूहों A तथा B पर विचार कीजिये। निम्न में से कौन-सा कथन सत्य है-
View Solutionएक अनभिनत पास को 6 बार उछाला जाता है। यदि एक समसंख्या प्राप्त करना एक सफलता है , तो
अधिक - से - अधिक 5 सफलताओ की प्रायिकता ज्ञात कीजिए।
View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
View Solutionएक बिंदु P, x-अक्ष पर और एक अन्य बिंदु Q, y-अक्ष पर स्थित है। (i) बिंदु P की कोटि ज्ञात कीजिए।
View Solutionएक पासे को फेंका जाता है। निम्नलिखित प्रत्येक घटना की प्रायिकता ज्ञात कीजिए।
(a) 2 से बड़ी एक संख्या प्राप्त करना
(b) अधिक-से-अधिक 4 प्राप्त करना
(c ) कम-से-कम 5 प्राप्त करना
View Solution30 बच्चो की एक कक्षा में सरन शीर्ष से 9 वे रैंक पर है| मनीष सरन से पांच रैंक निचे है| तल से मनीष की रैंक क्या है?
View Solution
