किसी समबाहु त्रिभुज ABC के प्रत्येक शीर्ष पर m kg तीन समान द्रव्यमान रखे है।
(a) इस त्रिभुज के केन्द्रक G पर रखे 2m kg के द्रव्यमान पर कितना बल आरोपित हो रहा है ?
(b) यदि शीर्ष A पर रखे द्रव्यमान को दो गुना कर दिया जाए, तो कितना बल आरोपित होगा ?
AG=BG=CG=1m लीजिए (देखिए चित्र)
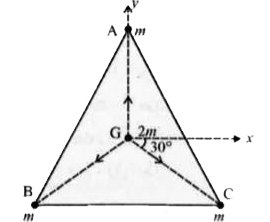
(a) चित्र की ज्यामिति से +X अक्ष तथा GC के मध्य कोण 30∘ बनता है तथा इतना ही कोण −X अक्ष तथा GB के मध्य बनता है। बिन्दु A पर स्थित m द्रव्यमान के कारण बिन्दु G पर स्थित 2m द्रव्यमान पर कार्यरत बल
→FGA=Gm×2m(AG)2 [GA के अनुदिश]
⇒→FGA=2m21ˆj ....(1)
बिन्दु B पर स्थित m द्रव्यमान के कारण बिन्दु G पर स्थित 2m द्रव्यमान पर कार्यरत बल
→FGB=Gm×2m(BG)2 [GB के अनुदिश]
⇒→FGB=2Gm21(−ˆicos30∘−ˆjsin30∘) ....(2)
बिन्दु C पर स्थित m द्रव्यमान के कारण बिन्दु G पर स्थित 2m द्रव्यमान पर कार्यरत बल
→FGC=Gm×2m(CG)2 [GC के अनुदिश]
⇒→FGC=2Gm21(ˆicos30∘−ˆjsin30∘) ......(3)
इस प्रकार बिन्दु G पर स्थित 2m द्रव्यमान पर परिणामी बल
→FG=→FGA+→FGB+→FGC
=2Gm2ˆj+2Gm2(−ˆicos30∘−ˆjsin30∘)+2Gm2(ˆicos30∘−ˆjsin30∘)
=2Gm2(ˆj−ˆicos30∘−ˆjsin30∘+ˆicos30∘−ˆjsin30∘)
=2Gm2(ˆj−2ˆjsin30∘)
=2Gm2(ˆj−ˆj)=0 [∵sin30∘=12]
(b) अब यदि बिन्दु A पर स्थित द्रव्यमान को दुगुना अर्थात 2m कर दिया जाये, तब
→FGA=G2m×2m(1)2ˆj=4Gm21ˆj
जबकि →FGB तथा →FGC अपरिवर्तित रहेंगे।
∴→FG=→FGA+→FGB+→FGC
=4Gm2ˆj+2Gm2(−ˆicos30∘−ˆjsin30∘)+2Gm2(ˆicos30∘−ˆjsin30∘)
=2Gm2(2ˆj−ˆj)=2Gm2ˆj
Topper's Solved these Questions
- गुरुत्वाकर्षण BOOK - SCIENCE PUBLICATIONCHAPTER - गुरुत्वाकर्षण EXERCISE - विविध उदाहरण
22 Videos
- गुरुत्वाकर्षण BOOK - SCIENCE PUBLICATIONCHAPTER - गुरुत्वाकर्षण EXERCISE - संभावित उदाहरण
8 Videos
- गति के नियम BOOK - SCIENCE PUBLICATIONCHAPTER - गति के नियम EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न )
38 Videos
- ठोसों के यांत्रिक गुण BOOK - SCIENCE PUBLICATIONCHAPTER - ठोसों के यांत्रिक गुण EXERCISE - अन्य महत्वपूर्ण प्र्शन आंकिक प्रशन (ऐंठन पर आधारित प्रशन)
1 Videos
Similar Questions
सूर्य से दो ग्रहों की दूरियाँ, क्रमशः 1013 तथा 1012 मीटर है ग्रहों के आवर्तकालों एवं इनकी चालों का अनुपात ज्ञात कीजिए।
View Solutionअपनी अक्ष पर पृथ्वी के घूमने की वह चाल ज्ञात कीजिए ताकि भूमध्य रेखा पर किसी मनुष्य का भार इस समय के भार का 3/5 हो जाये। भूमध्य रेखा पर पृथ्वी की त्रिज्या = 6400 किमी।
View Solution0.2 किग्रा. द्रव्यमान की क्रिकेट गेंद 20 मी./से. के वेग से गतिमान है। जिसे 0.4 सेकण्ड में विरामावस्था में लाया जाता है औसत बल की गणना कीजिए।
View Solutionl लम्बाई व r त्रिज्या की एक छड़, l/2 लम्बाई व r/2 त्रिज्या की समान पदार्थ की छड़ से जोड़ी जाती है| छोटी छड़ का मुक्त सिरा दृढ आधार पर कस दिया जाता है| लम्बी छड़ के मुक्त सिरे को θ कोण से मरोड़ा जाता है| दोनों छड़ों के जोड़ पर ऐंठन कोण का मान ज्ञात कीजिए|
View Solutionचार बिंदु आवेश qA=2μC,qB=−5μC,qc=2μC तथा qD=−5μC,10cm भुजा के किसी वर्ग ABCD के शीर्षो पर स्थित है । वर्ग के केंद्र पर रखे 1μC आवेश पर लगने वाला बल कितना है ?
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionयदि किसी त्रिभुज के शीर्षो के स्थिति सदिश क्रमश: →a,→b,→c हो तो इस त्रिभुज के केन्द्रक का स्थिति सदिश होगा -
View Solutionयदि किसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,0),(1,3) और (-1,2) हो तो उसके कोणों को ज्ञात कीजिए।
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionयदि किसी त्रिभुज के दो शीर्ष (6,4) ,(2,6) और केन्द्रक (4,6) हो जाए उसका तीसरा शीर्ष होगा
View Solution1 किग्रा, (32) किग्रा, एवं 2 किग्रा द्रव्यमानों के तीन कण a भुजा वाले एक समबाहु त्रिभुज के शीर्षों पर रखे गये हैं। द्रव्यमान केन्द्र के X, Y निर्देशांक होंगे-
View Solutionयदि दो समतल दर्पण 90^(@) के कोण पर रखे हो तो उनके मध्य कितने प्रतिबिम्ब बनेंगे
View Solution
