यदि किसी कृत्रिम उपग्रह का पृथ्वी के ठीक ऊपर चक्कर लगाने का परिक्रमण काल T तथा पृथ्वी का घनत्व ρ हो, तो सिद्ध कीजिए कि T=√3πGρ| इसकी सहायता से दर्शाइये कि T√ρ एक सार्वत्रिक नियतांक है। इस नियतांक का मान भी ज्ञात कीजिए। G=6.67×10−11 न्यूटन - मी.2/किग्रा.2
उपग्रह का परिक्रमण काल
T=2π√(r3GM)
पृथ्वी के ठीक ऊपर (h=0) उपग्रह की कक्षा की त्रिज्या
r=R+h≈R ∵h= नगण्य
∴T=2π√(R3GM)
पृथ्वी का द्रव्यमान
M = पृथ्वी का आयतन × घनत्व
=43πR2ρ
T=2π
⎷⎛⎝R3G.43πR3ρ⎞⎠=2π√(34πGρ)
या T=√(3πGρ) .....(1)
इससे T√ρ=(3πG)1/2 ....(2)
∵π तथा G सार्वत्रिक नियतांक है अतः (3πG)1/2= सार्वत्रिक नियतांक
∴T√ρ=(3πG)1/2= सार्वत्रिक नियतांक
=(3×3.146.67×10−11)1/2
=3.75×105किग्रा.1/2मी.3/2 सेकण्ड
Topper's Solved these Questions
- गुरुत्वाकर्षण BOOK - SCIENCE PUBLICATIONCHAPTER - गुरुत्वाकर्षण EXERCISE - विविध उदाहरण
22 Videos
- गुरुत्वाकर्षण BOOK - SCIENCE PUBLICATIONCHAPTER - गुरुत्वाकर्षण EXERCISE - संभावित उदाहरण
8 Videos
- गति के नियम BOOK - SCIENCE PUBLICATIONCHAPTER - गति के नियम EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न )
38 Videos
- ठोसों के यांत्रिक गुण BOOK - SCIENCE PUBLICATIONCHAPTER - ठोसों के यांत्रिक गुण EXERCISE - अन्य महत्वपूर्ण प्र्शन आंकिक प्रशन (ऐंठन पर आधारित प्रशन)
1 Videos
Similar Questions
सूर्य से दो ग्रहों की दूरियाँ, क्रमशः 1013 तथा 1012 मीटर है ग्रहों के आवर्तकालों एवं इनकी चालों का अनुपात ज्ञात कीजिए।
View Solutionअपनी अक्ष पर पृथ्वी के घूमने की वह चाल ज्ञात कीजिए ताकि भूमध्य रेखा पर किसी मनुष्य का भार इस समय के भार का 3/5 हो जाये। भूमध्य रेखा पर पृथ्वी की त्रिज्या = 6400 किमी।
View Solution0.2 किग्रा. द्रव्यमान की क्रिकेट गेंद 20 मी./से. के वेग से गतिमान है। जिसे 0.4 सेकण्ड में विरामावस्था में लाया जाता है औसत बल की गणना कीजिए।
View Solutionl लम्बाई व r त्रिज्या की एक छड़, l/2 लम्बाई व r/2 त्रिज्या की समान पदार्थ की छड़ से जोड़ी जाती है| छोटी छड़ का मुक्त सिरा दृढ आधार पर कस दिया जाता है| लम्बी छड़ के मुक्त सिरे को θ कोण से मरोड़ा जाता है| दोनों छड़ों के जोड़ पर ऐंठन कोण का मान ज्ञात कीजिए|
View Solutionएक इलेक्ट्रॉन (द्रव्यमान किग्रा) व एक प्रोटॉन (द्रव्यमान किग्रा) के बीच गुरुत्वाकर्षण-बल व स्थिरवैघुत बल का अनुपात ज्ञात कीजिए। (e=1.6×10−19 कूलाम तथा G=6.67×10−11 (न्यूटन-मीटर^(2)/किग्रा^(2))
View Solutionयदि 3+5r+7r2+……..∞=449 हो ,तो r का मान ज्ञात कीजिए ।
View Solutionआकृति के अनुसार यदि ∠BAC=80∘ हो तो ∠BCP का मान ज्ञात कीजिए।
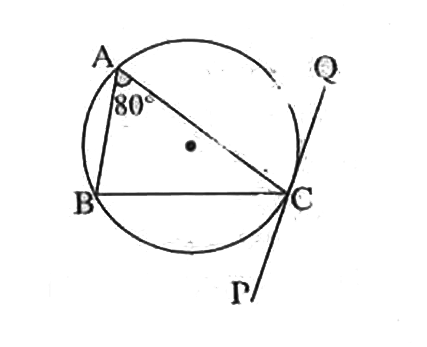
View Solutionसिद्ध कीजिए कि किसी गुणोत्तर श्रेढ़ी के आरम्भ और अंत से संदुररस्थ पदों का गुणनफलन सदैव अचर रहता है ।
View Solutionएक अनन्त गुणोत्तर श्रेढी का योग x है तथा श्रेढी के सभी पदों का वर्ग करने पर श्रेढी का योग y है । सिद्ध कीजिए कि श्रेढी का सार्व अनुपात x2−yx2+y है ।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionयदि z=(λ+3)+i√5−λ2 हो, तो सिध्द कीजिए कि z का बिन्दुपथ एक वृत्त होगा ।
View Solutionएक स्थिर आयतन वाले खुले टैंक का आधार वर्गाकार है। यदि अंत: पृष्ठ न्यूनतम हो, तब टैंक कि गहराई तथा लम्बाई का अनुपात ज्ञात कीजिए।
View Solutionदो पासे एक साथ फेंके जाते है।प्रायिकता ज्ञात कीजिए ऊपर जाने वाले अंको का योगफल 3 का गुणज हो।
View Solutionएक बहुविकल्पीय प्रश्न का उत्तर देने में विद्यार्थी या तो प्रश्न का उत्तर जानता है या जानता लगाता है | मान ले कि उसके उत्तर जान ने कि प्रायिकता 35 है तथा अनुमान लगाने कि प्रायिकता 25 है | मान ले कि छात्र के प्रश्न का उत्तर अनुमान लगाने पर सही उत्तर देने कि प्रायिकता 13 है , तो इसकी क्या प्रायिकता है कि कोई छात्र प्रश्न का उत्तर जानता है यदि यह ज्ञात है कि उसने सही उत्तर दिया है ?
View Solutionयदि x=asinθ तथा y=acosθ हो, तो सिद्ध कीजिए कि x2+y2=a2।
View Solution
