किसी पिण्ड को चिकने समतल पर ऊपर जाने में लगा समय t1 तथा वापस लौटने पर लगा समय t2 हो, तो t1 व t2 में सम्बन्ध ज्ञात कीजिए।
समतल के अनुदिश नीचे की ओर लगा त्वरण
a=gsinθ
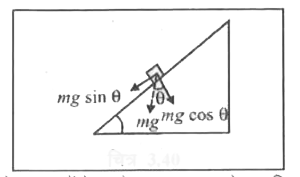
u वेग से ऊपर फेंके जाने पर, समतल के अनुदिश चली दूरी s हो, तो
सूत्र v2=u2+2as से ,
0=u2−2as
अर्थात् s=u22a
तथा v=u+at से
0=u−at1 अर्थात् u=at1
समीकरण (i) में u=at1 रखने पर,
s=(at1)22a=12at21
अतः ऊपर जाने में लगा समय
t1=√2sa
पिण्ड का ऊपर से नीचे वापस आने की स्थिति में
सूत्र s=ut+12at2 से
s=0+12at22
अर्थात् t2=√2sa
∴t1=t2
नोट-घर्षण बल होने की स्थिति में ऊपर व नीचे वापस आने की स्थिति में a का मान भिन्न होने के कारण, समय t1 व t2 अलग-अलग होंगे।
Topper's Solved these Questions
- सरल रेखा में गति BOOK - SCIENCE PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - NCERT TEXT BOOK PROBLEMS
22 Videos
- सरल रेखा में गति BOOK - SCIENCE PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - NCERT TEXT BOOK PROBLEMS (अतिरिक्त अभ्यास)
6 Videos
- सरल रेखा में गति BOOK - SCIENCE PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - विविध प्रश्न (Miscellaneous Problems) (अतिलघुत्तरात्मक प्रश्न)
6 Videos
- समतल में गति BOOK - SCIENCE PUBLICATIONCHAPTER - समतल में गति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)
29 Videos
Similar Questions
नीचे दिए गए गति के कौन से उदाहरणों में वस्तु को लगभग बिन्दु वस्तु माना जा सकता है:
(a) दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी।
(b) किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बंदर।।
(c) जमीन से टकराकर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद।
(d) किसी मेज के किनारे से फिसल कर गिरा कोई बीकर।
View Solutionकोई तीन पहिये वाला स्कूटर अपनी विरामावस्था से गति प्रारंभ करता है। फिर 10% तक किसी सीधी सड़क पर 1ms−2 के एकसमान त्वरण से चलता है। इसके बाद वह एकसमान वेग से चलता है। स्कूटर द्वारा n सेकंड (n = 1, 2, 3,........) में तय की गई दूरी को n के सापेक्ष आलेखित कीजिए। आप क्या आशा करते हैं कि त्वरित गति के दौरान यह ग्राफ कोई सरल रेखा या कोई परवलय होगा?
View Solutionएक विमीय गति में पिण्ड के विस्थापन का मान तथा पिण्ड द्वारा तय की गई दूरी में क्या सम्बन्ध है?
View Solutionदो बल 5 व 10 न्यूटन परस्पर 120∘ का कोण बनाते हुए स्थित है। उनके परिणामी बल का परिमाण व दिशा ज्ञात कीजिए।
View Solutiont1=(sinθ)cosθ,t2=(sinθ)sinθ,t3=(cosθ)cosθ,t4=(cosθ)sinθ (A) t3>t1>t2 (B) t4>t2>t1 (C) t4>t1>t2 (D) t1>t3>t2
View SolutionThe vertices of a triangle are [a t_1t_2,a(t_1 +t_2)], [a t_2t_3,a(t_2 +t_3)], [a t_3t_1,a(t_3 +t_1)] Then the orthocenter of the triangle is (a) (-a, a(t_1+t_2+t_3)-at_1t_2t_3) (b) (-a, a(t_1+t_2+t_3)+at_1t_2t_3) (c) (a, a(t_1+t_2+t_3)+at_1t_2t_3) (d) (a, a(t_1+t_2+t_3)-at_1t_2t_3)
View Solutionकुछ रसायनों के संपर्क में अधिक समय तक रहने पर, शरीर में पैदा ………………… हो सकती है
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutiony2=4ax என்ற பரவளையத்திற்கு 't1'மற்றும் 't2' ஆகிய புள்ளிகளில் அமையும் தொடுகோடுகள் [a't_1''t_2', 'a(t_1+t_2)']என்ற புள்ளியில் சந்திக்கின்றன என நிறுவுக.
View Solutionनिम्नलिखित में से किसी एक विषय पर दिए गए संकेत-बिन्दुओं के आधार पर 200 से 250 शब्दों में निबन्ध लिखिए। बीता समय फिर लौटता नहीं $ समय का महत्त्व $ समय नियोजन $ समय गँवाने की हानियाँ
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+at1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is: (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+a(t1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View Solutionp - V diagram of same mass of a gas are drawn at two different temperatures (T_1) and (T_2) . Explain whether T_1 gt T_2 or T_2 gt T_1 . .
View SolutionShow that the points (at21,2at1)(at22,2at2) and (a,0) are collinear if t1t2=−1
View SolutionArea of the triangle formed by the threepoints 't1'.'t2'and't3' on y2=4ax is K|(t1−t2)(t2−t3)(t3−t1)| then K=
View SolutionThe normal drawn at a point (at21,−2at1) of the parabola y2=4ax meets it again in the point (at22,2at2), then t2=t1+2t1 (b) t2=t1−2t1 t2=−t1+2t1 (d) t2=−t1−2t1
View Solution
