एकविमीय गति में किसी कण का वेग-समय ग्राफ चित्र में दिखाया गया है
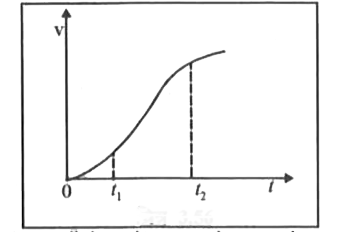
नीचे दिए सूत्रों मे से तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही हैं-
(i) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(ii) v(t2)=v(t1)+a(t2−t1)
(iii) vaverage=[x(t2)−x(t1)]/(t2−t1)
(iv) aaverage=[v(t2)+v(t1)]/(t2−t1)
(v)x(t2)=x(t1)+Vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(vi) x(t2_=t अक्ष तथा दिखाई गई बिन्दुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल।
दिए गए आरेख से स्पष्ट है कि वक्र का ढाल स्थिर तथा एक समान नहीं है अतः सम्बन्ध (i), (ii) तथा (v) सही नहीं है जबकि सम्बन्ध (iii), (iv) तथा (vi) सही है।
Topper's Solved these Questions
- सरल रेखा में गति BOOK - SCIENCE PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (लघुत्तरात्माक प्रश्न)
5 Videos
- सरल रेखा में गति BOOK - SCIENCE PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न निबन्धात्मक प्रश्न
1 Videos
- सरल रेखा में गति BOOK - SCIENCE PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - NCERT TEXT BOOK PROBLEMS
22 Videos
- समतल में गति BOOK - SCIENCE PUBLICATIONCHAPTER - समतल में गति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)
29 Videos
Similar Questions
निम्न की परिभाषा देकर अन्तर स्पष्ट कीजिये
(i) दूरी और विस्थापन (ii) औसत चाल और औसत वेग
(iii) तात्क्षणिक वेग और तात्क्षणिक त्वरण।
View Solutionएक समान त्वरित एक विमीय गति के लिये गति की तीनों समीकरणों को व्युत्पन्न कीजिये।
View Solutionनीचे दिए गए गति के कौन से उदाहरणों में वस्तु को लगभग बिन्दु वस्तु माना जा सकता है:
(a) दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी।
(b) किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बंदर।।
(c) जमीन से टकराकर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद।
(d) किसी मेज के किनारे से फिसल कर गिरा कोई बीकर।
View Solutionदो बल 5 व 10 न्यूटन परस्पर 120∘ का कोण बनाते हुए स्थित है। उनके परिणामी बल का परिमाण व दिशा ज्ञात कीजिए।
View Solutiont1=(sinθ)cosθ,t2=(sinθ)sinθ,t3=(cosθ)cosθ,t4=(cosθ)sinθ (A) t3>t1>t2 (B) t4>t2>t1 (C) t4>t1>t2 (D) t1>t3>t2
View SolutionThe vertices of a triangle are [a t_1t_2,a(t_1 +t_2)], [a t_2t_3,a(t_2 +t_3)], [a t_3t_1,a(t_3 +t_1)] Then the orthocenter of the triangle is (a) (-a, a(t_1+t_2+t_3)-at_1t_2t_3) (b) (-a, a(t_1+t_2+t_3)+at_1t_2t_3) (c) (a, a(t_1+t_2+t_3)+at_1t_2t_3) (d) (a, a(t_1+t_2+t_3)-at_1t_2t_3)
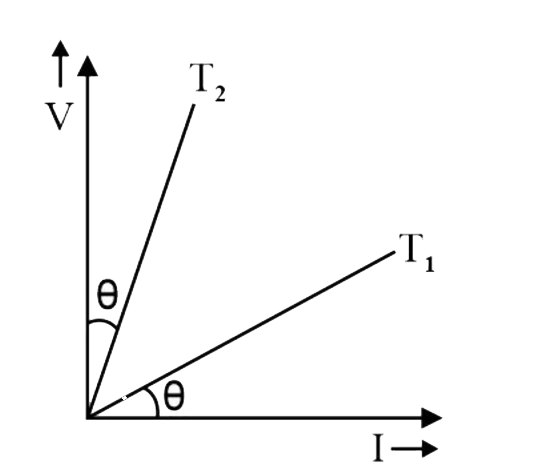
View SolutionThe V-i graph for a conductor at temeratures T_1 and T_2 are as shown in the figure. (T_2 - T_1) is alphaortional to. .
View SolutionThe V - I graphs for a conductor at temperature T1andT2 are shown in the figure (T2−T1) is proportional to
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+at1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is: (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+a(t1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View Solutionp - V diagram of same mass of a gas are drawn at two different temperatures (T_1) and (T_2) . Explain whether T_1 gt T_2 or T_2 gt T_1 . .
View SolutionShow that the points (at21,2at1)(at22,2at2) and (a,0) are collinear if t1t2=−1
View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in Fig. 3.29 :-Which of the following formulae are correct for describing the motion of the particle over the time-interval t_1 to t_2 :- x(t_2)=x(t_1)+v(t_1)(t_2-t_1)+(1/2)a(t_2-t_1)^2
View SolutionFor any arbitrary motion in space, which of the following relations are true :- aaveragv(t2)−v(t1)t2−t1(The ‘average’ stands for average of the quantity over the time interval t1→t2)
View SolutionThe normal drawn at a point (at21,−2at1) of the parabola y2=4ax meets it again in the point (at22,2at2), then t2=t1+2t1 (b) t2=t1−2t1 t2=−t1+2t1 (d) t2=−t1−2t1
View SolutionThe vertices of a triangle are [a t_1t_2,a(t_1 +t_2)] , [a t_2t_3,a(t_2 +t_3)] , [a t_3t_1,a(t_3 +t_1)] Then the orthocenter of the triangle is (a) (-a, a(t_1+t_2+t_3)-at_1t_2t_3) (b) (-a, a(t_1+t_2+t_3)+at_1t_2t_3) (c) (a, a(t_1+t_2+t_3)+at_1t_2t_3) (d) (a, a(t_1+t_2+t_3)-at_1t_2t_3)
View Solution
