मूल सिद्धान्त के आधार पर समीकरण ω=ω0+αt व्युत्पन्न कीजिए।
कोणीय त्वरण α अचर है
अतः α=dωdt= नियतांक
समाकलन करने पर
∫dω=∫αdt+C
यहाँ C = समाकलन नियतांक
⇒ω=αt+C...(1)∴ अचर है।
प्रश्नानुसार t=0 पर ω=ω0
∴ω0=0+C=C
∴ ω0=0+C+C
∴ समी. (1) से ω=αt+ω0
⇒ω=ω0+αt
Topper's Solved these Questions
- कणों के निकाय तथा घूर्णी गति BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - TEST YOUR KNOWLEDGE
20 Videos
- कणों के निकाय तथा घूर्णी गति BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - MCQs
11 Videos
- उष्मागतिकीBOOK - SCIENCE PUBLICATIONCHAPTER - उष्मागतिकीEXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)
28 Videos
- कार्य, ऊर्जा एवं शक्ति BOOK - SCIENCE PUBLICATIONCHAPTER - कार्य, ऊर्जा एवं शक्ति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकित प्रश्न ) टक्करों पर आधारित प्रश्न
8 Videos
Similar Questions
घूर्णन गति से क्या तात्पर्य है?
View Solutionयदि HCI अणु में H' की द्रव्यमान-केन्द्र से दूरी x हो तो CI35 की दूरी होगी
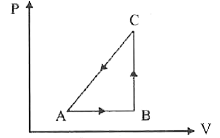
View Solutionएक निकाय का P-V आरेख जो कि ऊष्मागतिकी परिवर्तन प्रदर्शित करता है। चित्र में दर्शाया गया है। निकाय पर किया गया कार्य A→B→C 50J है ,आंतरिक ऊर्जा में परिवर्तन ज्ञात कीजिये,दी गई ऊष्मा 84 J है।
View Solutionदो किलोग्राम द्रव्यमान का एक पिण्ड किसी अन्य स्थिर पिण्ड से पूर्णतः अप्रत्यास्थ टक्कर करता है। यदि टक्कर के बाद दोनों पिण्ड उसी दिशा में पहले पिण्ड की एक चौथाई चाल से गतिमान हो तो दुसरे पिण्ड का द्रव्यमान ज्ञात करिये।
View Solutionनिम्नलिखित जानकारी के आधार पर विज्ञापन का प्रारूप तैयार कीजिए : संपर्क घर किराये पर देना विशेषताएँ
View Solutionनिम्न वक्रो के लिए उनके सम्मुख अंकित बिंदु पर स्पर्श रेखा एवं अभिलम्ब के समीकरण ज्ञात कीजिए-
xy=a2,(at,at)
View Solutionयदि समीकरण 3x2−6x+5=0 के मूल α,β हो, तो वह समीकरण जिसके मूल α+β व् 2α+β है, होगा
View Solutionयदि α,β द्विघात समीकरण x2+px+p3=0(p≠0) के मूल हो तथा (α,β) परवलय y2=x पर स्थित एक बिंदु हो, तो समीकरण के मूल होगा
View Solutionयदि समीकरण x2−px+q=0 के मूल secα व cosecα है, तब
View Solutionयदि समीकरण px2+qx+r=0 के मूल sinα व cosα हों, तो
View Solutionकाव्यांश के आधार पर परशुराम के स्वभाव की दो विशेषताओं पर सोदाहरण टिप्पणी कीजिए।
View Solutionद्विघात समीकरण के मूल|द्विघात समीकरण के मूलों की प्रकृति
View Solutionसमीकरण के मूल
View Solutionसमीकरण के मूल
View Solutionसमीकरण के मूल
View Solution
