किसी 'व्युत्क्रम-वर्ग' क्षेत्र (जैसा कि रदरफोर्ड मॉडल में आवेशित नाभिक द्वारा उत्पन्न होता है) द्वारा प्रकीर्णन के लिए संघट्ट पैरामीटर b और प्रकीर्णन कोण θ के बीच सम्बन्ध है:
b=Ze2cot(θ/2)4πε0(12mv2)
(a) b=0 के लिए प्रकीर्णन कोण क्या है?
(b) दिए गए संघट्ट पैरामीटर b के लिए विक्षेपण कोण, ऊर्जा में वृद्धि के साथ बढ़ता है या घटता है?
(c ) वह संघट्ट पैरामीटर कितना है जिस पर Z = 79 के लिए प्रकीर्णन कोण 90∘ है और आरम्भिक ऊर्जा 10 MeV?
(d) ऐसा क्यों है कि नाभिक का आवेश, उपरोक्त सूत्र में आता है परन्तु द्रव्यमान नहीं आता?
(e) प्रक्षेपित वस्तु की दी गई ऊर्जा के लिए क्या संघट्ट पैरामीटर के घटने से प्रकीर्णन कोण बढ़ता है या घटता है?
(a) जब b = 0, तो cot(θ/2)=0
या (θ/2)=90∘
या θ=180∘
अर्थात ऐल्फा-कण, 180∘ के कोण से प्रकीर्णित होता है।
इस स्थिति में यह अपने आरम्भिक पथ के अनुदिश परावर्तित हो जाता है। स्पष्टतया, इसी शर्त के अन्तर्गत कण का नाभिक की ओर निकटतम उपगमन होगा।
(b) b के दिए गए मान के लिए
Ze2cot(θ/2)4πε0(12mv2) = स्थिरांक
जब ऊर्जा (12mv2) बढ़ती है, तो cot(θ/2) भी बढ़ता है और परिणाम स्वरूप θ घटता है।
(c) b=Ze2cot(θ/2)4πε0(12mv2)
=(9×109)79(1.6×10−19)2cot(90∘2)10(1.6×10−13)m
=1.14×10−14m
(d) यदि Z = 0, तो θ=0 अर्थात नाभिक का आवेश ही प्रकीर्णन उत्पन्न करता है। वास्तव में नाभिक का आवेश ही प्रकीर्णन के लिए वैद्युत क्षेत्र उपलब्ध करवाता है और इसीलिए यह सूत्र में आता है। प्रकीर्णन के कारण नाभिक प्रतिक्षेपित होता है। परन्तु क्योकि हम नाभिक के प्रतिक्षेप की उपेक्षा करते है, इसलिए इसका द्रव्यमान सूत्र में नहीं आता है। यदि नाभिक के प्रतिक्षेप की उपेक्षा नहीं करनी है, तो नाभिक का द्रव्यमान, दिए गए सूत्र में एक छोटे से संशोधन पद में प्रकट होता है।
(e) जब प्रक्षेप्य की ऊर्जा (12mv2) दी गई हो, तो
cot(θ/2)∝b
या tan(θ/2)∝1b
या θ∝1b
इस प्रकार b के घटने से θ बढ़ता है।
Topper's Solved these Questions
- परमाणुBOOK - GRB PUBLICATION HINDICHAPTER - परमाणुEXERCISE - प्रश्नोत्तरी : 1 अंक
14 Videos
- परमाणुBOOK - GRB PUBLICATION HINDICHAPTER - परमाणुEXERCISE - प्रश्नोत्तरी : 2 और 3 अंक
19 Videos
- परमाणुBOOK - GRB PUBLICATION HINDICHAPTER - परमाणुEXERCISE - विषय-आधारित समस्याएँ : हल सहित
28 Videos
- नाभिक BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (रिक्त स्थान भरना )
25 Videos
- प्रकाशिक यन्त्रBOOK - GRB PUBLICATION HINDICHAPTER - प्रकाशिक यन्त्रEXERCISE - NCERT पाठ्यपुस्तक अभ्यास
8 Videos
Similar Questions
टॉमसन का परमाणु मॉडल क्यों असफल रहा?
View Solutionगाइगर-मार्सडन प्रयोग में अलग-अलग ऐल्फा-कणो द्वारा अनुरेखित प्रक्षेप-पथ, चित्र 18.4 में दर्शाये अनुसार देखे गए।
(a) यहाँ दिखाए गए प्रतीकों b और θ के क्या नाम है?
(b) (i) θ=0∘ और (ii) θ=π rad के लिए 'b' के मानों के बारे में हम क्या कह सकते है?
View Solutionजब एक 5.0 MeV प्रोटॉन, स्वर्ण के नाभिक (Z = 79) की ओर जाता है, तो निकटतम उपगमन की दूरी क्या होगी?
View Solutionएक परमाणु में दो इलेक्ट्रॉन , नाभिक के गिर्द R और 4R व्यासार्धों वाली वृत्ताकार कक्षाओं में घूमते हैं। और चक्कर पूरा करने के लिए उनके द्वारा लिए गए समयों का अनुपात ................ है।
View Solutionएक छोटे दूरदर्शक के अभिदृश्यक लेन्स की फोकस दुरी 144cm , और नेत्रिका की 6.0cm है। दूरदर्शक की आवर्धन क्षमता क्या है ? अभिदृश्यक और नेत्रिका के बीच कितनी दुरी है ?
View Solutionλ के वे मान ज्ञात कीजिए जिनके लिए सदिशों ¯a=2λ2ˆi+4λˆj+ˆk और ¯b=7ˆi−2ˆj+λˆk के बीच का कोण अधिक कोण है ।
View Solutionकोई रेखा x-अक्ष और y-से साथ क्रमशः 60∘ तथा 45∘ के कोण बनाती है। इनके द्वारा घनत्व दिशा में z-अक्ष के साथ कितना कोण बनेगा ?
View Solutionचित्र में दिखाए गए छायांकित क्षेत्र के लिए असामिका है-
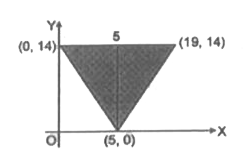
View Solutionλ और μ के जिस मान के लिए सदिश a=2ˆi+λˆj−ˆk , सदिश b=3ˆi+ˆj−μˆkके लम्ब है तथा |a|=|b| है , वः मान है
View SolutionIf '-' stands for addition, 'div' for multiplication, 'xx' for subtraction, and '+' for division, then which of there following is correct? यदि '-' जोड़ के लिए है, 'div' गुणा के लिए, 'xx' घटाने के लिए है और '+' भाग के लिए है तो निम्नलिखित में से क्या सही है?
View SolutionIf '+' stands for'+', '-' stands for '=', 'x' stands for '+', '+' stands for greater than, '=' stands for less then, '>' stands for multiplication and '<' stands for subtraction, then which of the following alternatives is correct?
View Solution(Na_2CO_3+NaHCO_3) के मिश्रण में अनुमापन के लिए HCL की आवश्यक मात्रा फेनोल्फथेलिन सूचक के साथ x mL है और मिथाइल ऑरेंज सूचक के साथ y mL है अतः Na_2CO_3 की पूर्ण अभिक्रिया के लिए HCL का आयतन है
View Solutionअभिक्रिया A (g)=B(g)iff C(g) के लिए Kc और Kp के बीच संबंध है:
View Solutionशून्य कोटि अभिक्रिया के लिए, सांद्रता और समय के बीच का आरेख निम्न के साथ रेखीय होता है:
View Solutionयदि Br_2 (l) के लिए कणन एन्थैल्पी x kJ/mol है और Br_2 के लिए बंध एन्थैल्पी y kJ/mol है, तो उनके बीच संबंध है कि -
View Solutionरदरफोर्ड के α -कण प्रकीर्णन प्रयोग से क्या निष्कर्ष निकलता है?
View Solution
