जब एक कण को X - क्षय के अनुदिश x = 0 और x = a के बीच चलने के लिए प्रतिबंधित किया जाता है , जहाँ a, नैनोमीटर विमा का है , तो इसकी ऊर्जा के केवल कुछ विशिष्ट मान ही हो सकते हैं। ऐसे प्रतिबिंब क्षेत्र में चल रहे कण की अनुमत ऊर्जाऍं , अप्रगामि तरंगों की रचना के संगत होती है जिनके नोड इसके सिरों x = 0 और x = a पर है। इस अप्रगामि तरंग का तरंगदैर्ध्य , कण के रेखीय संवेग p के साथ दे ब्रॉग्ली सम्बन्ध के अनुसार सम्बन्धित है। m द्रव्यमान वाले कण की ऊर्जा, इसके रेखीय संवेग के साथ E=p22m के अनुसार सम्बन्धित है। इस प्रकार कारण ऊर्जा एक , क्वान्टम संख्या n द्वारा निर्दिष्ट की जा सकती है जिसमें n के मान 1,2,3,..............(n =1 को निम्नतम अवस्था कहते हैं होते हैं जो अप्रगामी तरंग में लूपों की संख्या के संगत होते हैं।
उपरोक्त वर्णित मॉडल का प्रयोग, रेखा x = 0 से x = a में चल रहे कल के लिए निम्न तीन प्रश्नों के उत्तर देने के लिए करें |
h=6.6×10−34Js और e=1.6×10−19C लें |
कण के लिए n के किसी विशेष मान के लिए अनुमत ऊर्जा अनुपाती है
a−2
a−3/2
a−1
a2
The correct Answer is:A
क्योंकि a=nλ/2 , इसलिए λ=2a/n और दी ब्रॉग्ली तरंगदैर्ध्य λ=h/p,
इसलिए 2an=hp या p=nh2a
कण के लिए अनुमत ऊर्जा E=p22m=n2h28a2m
जहाँ से E∝1a2 अर्थात E∝a−2
Topper's Solved these Questions
- नाभिक BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (कॉलम मिलाना)
7 Videos
- नाभिक BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (कथन - कारण - आधारित प्रश्न )
20 Videos
- नाभिक BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (बहुविकल्पीय प्रश्न: एक सही विकल्प )
155 Videos
- धारिता और परावैधुत पदार्थ BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (रिक्त स्थान भरना )
15 Videos
- परमाणुBOOK - GRB PUBLICATION HINDICHAPTER - परमाणुEXERCISE - NCERT पाठ्यपुस्तक अभ्यास उत्तरो सहित
16 Videos
Similar Questions
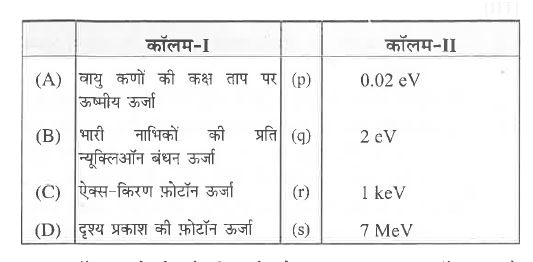
कॉलम - I की सूची में दी गई भौतिक राशियों को कॉलम - II की सूची में यादृच्छिक रूप से दिए गए उनके मानों के साथ मिलाएँ।
View SolutionA : बोर की अभिगृहीत प्रस्तुत करना पड़ा कि नाभिक के गिर्द स्थिर कक्षाओं में इलेक्ट्रॉनों से विकिरण नहीं होता।
R: कलॉसिकी भौतिक के अनुसार सभी गतिमान इलेक्ट्रॉन वितरण उत्पन्न करते हैं।
View Solutionइन समूहों में से किसमें प्रथम कक्षा (n = 1 ) का व्यासार्ध निम्नतम होगा ?
View Solutionएकसमान धनात्मक आवेश Q (कूलॉम) वाली दो छोटी गेंदे एक स्टैण्ड से जुडी एक हुक के साथ L (मीटर ) लम्बी दो विधुतरोधी डोरियों से लटकाई जाती है। यह समूह उपग्रह द्वारा अंतरिक्ष में ले जाय जाता है जहाँ कोई गुरुत्व नहीं (भारहीनता की स्थिति ) है। दोनों डोरियों के बीच कोण .......... है और दोनों डोरियों में तनाव ........ न्यूटन है।
View Solutionटॉमसन मॉडल में परमाणु का साइज रदरफोर्ड मॉडल में परमाण्विक साइज से है। (बहु ज्यादा/कोई अलग नहीं/काफी कम)
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solution(Na_2CO_3+NaHCO_3) के मिश्रण में अनुमापन के लिए HCL की आवश्यक मात्रा फेनोल्फथेलिन सूचक के साथ x mL है और मिथाइल ऑरेंज सूचक के साथ y mL है अतः Na_2CO_3 की पूर्ण अभिक्रिया के लिए HCL का आयतन है
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solution1.0 mg के द्रव्यमान वाले एक कण का वेग 3600 km/h है। कण के तरंग दैर्ध्य की गणना कीजिए।
View Solution1.44g टाइटेनियम (Ti) की O_(2) के आधिक्य के साथ अभिक्रिया होती है और एक अरससमीकरणमितीय यौगिक Ti_(1.44)O_(1) के x g का निर्माण होता है। तो x का मान g में होगा :
View Solutionजब AgNO_(3) के विलयन को आधिक्य में CoCl_(3).XNH_(3) विलयन के 1M में मिलाया जाता है, तो AgCI के एक मोल का निर्माण होता है? 'X' का मान क्या है? (माना लीजिए कि उपसहसंयोजन संख्या 6 है।)
View Solutionएक यौगिक (A) का उपयोग सॉल्वे प्रक्रम में अमोनिया की पुनः प्राप्ति के लिए धावन सोडा के विचरन में किया जाता है। जब CO_(2) को (A) के जलीय विखंडन में बुदबुदाया जाता है तो विलयन दूधिया हो जाता है। इसका उपयोग विसंक्रामक प्रकृति के कारण सफेदी में किया जाता है। A का रासायनिक सूत्र क्या होगा?
View Solutionसंगलित अशुद्ध धातु को लकड़ी के हरे रंग के लट्टे के साथ हिलाकर फफोलेदार तांबा को परिष्कृत किया जाता है, क्योंकि इस प्रकार की लकड़ी, हाइड्रोकार्बन गैसों (जैसे CH_4 ) को मुक्त करती है। इस प्रक्रम X को ________ कहा जाता है और इसका उपयोग धातु में प्रारंभ में उपस्थित Y की अशुद्धियों के शुद्धिकरण के लिए किया जाता है। Y _______ है।
View Solutionनाइट्रोजन युक्त कार्बनिक यौगिक के 29.5 mg को केल्डॉल विधि द्वारा उपचारित किया जाता है और मुक्त अमोनिया को 0.1 M HCI विलयन के 20mL में अवशोषित किया जाता है। अम्ल के आधिक्य के पूर्ण उदासीनीकरण के लिए 0.1M NaOH विलयन के 15mL की आवश्यकता होती है। यौगिक में नाइट्रोजन की प्रतिशतता है
View Solutionऐलुमिनो-तापीय प्रक्रम का उपयोग उन धातुओं के निष्कर्षण के लिए किया जाता है, जिनके ऑक्साइड-
View Solutionबोश प्रक्रम का उपयोग हाइड्रोजन गैस के उत्पादन के लिए किया जाता है, दी गई गैस में से किस गैस का उपयोग इसके लिए किया जाता है
View Solution
