△PQR की भुजा QR पर एक बिन्दु T है एवं कोई एक बिन्दु S इस प्रकार है कि RT = ST, सिद्ध करें कि PQ+PR>QS
Step by step video & image solution for trianglePQR की भुजा QR पर एक बिन्दु T है एवं कोई एक बिन्दु S इस प्रकार है कि RT = ST, सिद्ध करें कि PQ + PR gt QS by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुजों की सर्वागसमता एवं त्रिभुजों में असमानता BOOK - ALOK BHARTI PUBLICATIONCHAPTER - त्रिभुजों की सर्वागसमता एवं त्रिभुजों में असमानता EXERCISE - प्रश्नावली (Exercise) 9 (अतिलघु उत्तरीय प्रश्न )
20 Videos
- त्रिभुजों की सर्वागसमता एवं त्रिभुजों में असमानता BOOK - ALOK BHARTI PUBLICATIONCHAPTER - त्रिभुजों की सर्वागसमता एवं त्रिभुजों में असमानता EXERCISE - प्रश्नावली (Exercise) 9 (बहुविकल्पीय प्रश्न)
5 Videos
- त्रिभुज एवं चतुर्भुज के क्षेत्रफलBOOK - ALOK BHARTI PUBLICATIONCHAPTER - त्रिभुज एवं चतुर्भुज के क्षेत्रफलEXERCISE - प्रश्नावली (14.2) दीर्घ उत्तरीय प्रश्न
17 Videos
- दो चरों वाले रैखिक समीकरणBOOK - ALOK BHARTI PUBLICATIONCHAPTER - दो चरों वाले रैखिक समीकरणEXERCISE - प्रश्नवाली 4.2 (लघु उत्तरीय प्रश्न)
14 Videos
Similar Questions
किसी त्रिभुज के दो कोण समान हों तो वह त्रिभुज ______ होगा।
View Solutionयदि किसी त्रिभुज के आधार को दोनों ओर बढ़ाने पर प्रत्येक बहिष्कोण 130∘ का हो तो वह त्रिभुज किस प्रकार का त्रिभुज होगा?
View Solutionकिसी चतुर्भुज की भुजाएं क्रमानुसार 5 सेमी, 12 सेमी, 14 सेमी एवं 15 सेमी है। यदि प्रथम दो भुजाओं के बीच का कोण समकोण हो तो चतुर्भुज का क्षेत्रफल ज्ञात करें।
View Solutionनिम्नलिखित समीकरणों के आलेख खींचें।
View SolutionIn Figure, T is a point on side QR of PQR and S is a point such that RT=ST. Prove That : PQ+PR>QS
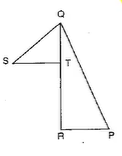
View SolutionΔPQRकी भुजा QR पर कोई बिन्दु T है तथा S कोई बिन्दु ऐसा है कि RT=ST,तो सिध्द करो कि PQ+PR>QS.
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionकोई फलन किसी बिन्दु x = a पर अवकलनीय कहलता है, जब -
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। प्रायिकता ज्ञात कीजिए कि 5 कदम चलने के पश्चात, यह व्यक्ति प्रारम्भिक बिन्दु से एक कदम दूर है।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionयदि बिन्दु P(−3,4) से होकर जाने वाली एक सरल रेखा इस प्रकार है कि इसके निर्देशांक अक्षो के बीच अंत: खंडित भाग का मध्य -बिन्दु P है, तो इसका समीकरण है
View Solutionयदि एक बल →F=3ˆi+2ˆj−4ˆk एक बिन्दु P(1,-1,2) पर कार्यरत है, तब बिन्दु Q(2, -1, 3) के सापेक्ष →F का आघूर्ण है
View Solution
