एक पैराशूटधारी कूदने के पश्चात् 50m बिना घर्षण (प्रतिरोध) के गिरता है। जब पैराशूट खुलता है तो यह से अवमंदित होता है। यदि वह पृथ्वी तल पर 3 m/s के वेग से पहुँचता है, तो वह कितनी ऊँचाई से कूदा था
293 m
111m
91m
182m
The correct Answer is:A
बिन्दु A से कूदने के पश्चात् पैराशूटधारी मुक्त रूप से गुरुत्व के प्रभाव में गति करता है। माना बिन्दु B पर इसके द्वारा प्राप्त वेग .v. है
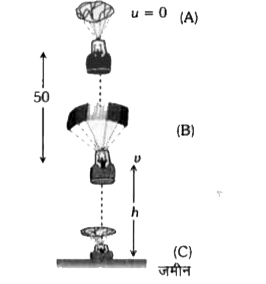
का प्रयोग करने पर
[ क्योंकि
बिन्दु B पर, पैराशूट खुल जाता है तथा यह के मंदन से । गिरता है, तथा जमीन पर (C बिन्दु पर) 3m/s से पहुंचता है। .BC. भाग के लिये, समीकरण का प्रयोग करने पर
अतः पैराशुटधारी द्वारा तय की गयी कुल ऊँचाई = 50+243 = 293 m.
Topper's Solved these Questions
- एक विमीय गति BOOK - ERRORLESS HINDICHAPTER - एक विमीय गति EXERCISE - GRAPHICAL QUESTIONS OBJECIVE QUESTIONS
30 Videos
- एक विमीय गति BOOK - ERRORLESS HINDICHAPTER - एक विमीय गति EXERCISE - JEE SECTION (MORE THAN ONE CORRECT ANSWERS)
3 Videos
- एक विमीय गति BOOK - ERRORLESS HINDICHAPTER - एक विमीय गति EXERCISE - ORDINARY THINKING OBJECTIVE QUESTIONS (गुरुत्व के अधीन गति )
53 Videos
- ऊष्मागतिक प्रक्रम BOOK - ERRORLESS HINDICHAPTER - ऊष्मागतिक प्रक्रम EXERCISE - SELF EVALUATION TEST
15 Videos
- कार्य, ऊर्जा, शक्ति एवं संघट्ट BOOK - ERRORLESS HINDICHAPTER - कार्य, ऊर्जा, शक्ति एवं संघट्ट EXERCISE - SELF EVALUATION TEST
19 Videos
Similar Questions
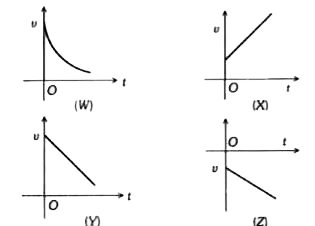
नीचे दिये गये चार वक्र एक वस्तु के वेग तथा समय के मध्य विभिन्नता दर्शाते हैं। निम्न में से कौन सा आरेख यह दर्शाता है कि वस्तु की प्रारंभिक गति धनात्मक दिशा में स्थिर ऋणात्मक त्वरण के साथ है
View Solutionमाना एक विमीय गति में किसी पिण्ड का वेग तथा त्वरण क्रमशः →v तथा →a के द्वारा प्रदर्शित किए जाते हैं, तब
View Solutionदो पिण्ड ऊर्ध्वाधर ऊपर की दिशा में 2 : 3 के अनुपात की प्रारम्भिक चाल से फेंके जाते हैं। इनके द्वारा तय अधिकतम ऊँचाई का अनुपात तथा पृथ्वी सतह पर लौटने में लगे समय का अनुपात क्रमशः हैं
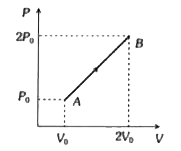
View Solutionएक प्रक्रम A→B के लिए, 2 ग्राम हीलियम गैस का PV वक्र चित्र में दिखाया गया है। प्रक्रम A→B में गैस को दी गई ऊष्मा है
View Solutionएक गेंद बिना फिसले रहित झुकी टेबल पर गति करती है टेबल की सतह द्वारा गेंद पर संपन्न कार्य है
View Solution60km/h के वेग से चलती मोटरसाइकिल का जड़त्व 20 km //h के वेग से चलती मोटरगाड़ी के जड़त्व से …………… होता है।
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
View Solutionनिर्देशानुसार उत्तर दीजिए :
जब-जब वह यहाँ आता है तो पढ़ाई के बारे में चर्चा करता है।
(रचना के आधार पर वाक्य भेद बताइए)
View Solutionक्रोध दुख के चेतन कारण से साक्षात्कार या अनुमान से उत्पन्न होता है। साक्षात्कार के समय दुख और उसे कारण का परिज्ञान आवश्यक है। तीन-चार महीने के बच्चे को कोई हाथ उठाकर मार दे, तो उसके हाथ उठते तो देखा है पर अपनी पीड़ा और उस हाथ उठाने में क्या संबंध है, यह वह नहीं जानता है। अतः वह केवल रोकर अपना दुख मात्र प्रकट कर देता है। दुख के कारण की स्पष्ट धारणा के बिना क्रोध का उदय नहीं होता है। दुख के सज्ञान कारण पर प्रबल प्रभाव डालने में प्रवृत्त करने वाला मनोविकार होने के कारण क्रोध का अविर्भाव बहुत पहले देखा जाता है। शिशु अपनी माता की आकृति से परिचित हो जाने पर ज्योंही यह जान जाता है कि दूध इसी से मिलता है. भूख होने पर उसे देखते ही अपने रोने में कुछ क्रोध का आभास देने लगता है।
क्रोध एक प्रकार का है।
View Solutionजिनका उच्चारण ऊपर के दांतो पर जीभ लगाने से होता है, उन्हें क्या कहते है ?
View Solutionएक 5 kg द्रव्यमान वाली वस्तु पर 2s के लिये एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3m/s से बढा 7m/s कर देता है। लगाये गये बल की मात्रा ज्ञात करें
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View SolutionIf '+' stands for'+', '-' stands for '=', 'x' stands for '+', '+' stands for greater than, '=' stands for less then, '>' stands for multiplication and '<' stands for subtraction, then which of the following alternatives is correct?
View SolutionStudy the following information carefully and answer the given questions : Eight person P, Q, R, S, T, U, V and W are seated around a circular table. Three among them are facing towards centre and they are not seated next to each other. R and S are not immediate neighbours of W and P. R is facing that direction in which W is facing. P is fourth to the left of W and both are facing to each other. T is to the immediate right of R. T and Q are not immediate neighbours of P. If V is to the left of s, then who among the following is / are seated between P and T?
View Solution
