Doubtnut Promotions Sticky

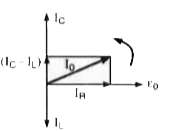
स्रोत की आवृत्ति, श्रेणीक्रम LCR परिपथ की अनुनादी आवृत्ति के बराबर रखते हुए यदि तीन अवयव L,C और R समान्तर में रखे जाते है, तो सिद्ध करें कि समान्तर LCR परिपथ में इस आवृत्ति पर कुल धारा न्यूनतम है। इस आवृत्ति के लिए प्रश्न 7.11 में वर्णित अवयवों और स्रोत के लिए परिपथ की हर शाखा में धारा का rms मान प्राप्त करें।
स्रोत की आवृत्ति, श्रेणीक्रम LCR परिपथ की अनुनादी आवृत्ति के बराबर रखते हुए यदि तीन अवयव L,C और R समान्तर में रखे जाते है, तो सिद्ध करें कि समान्तर LCR परिपथ में इस आवृत्ति पर कुल धारा न्यूनतम है। इस आवृत्ति के लिए प्रश्न 7.11 में वर्णित अवयवों और स्रोत के लिए परिपथ की हर शाखा में धारा का rms मान प्राप्त करें।

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

क्योंकि किन्हीं दो विन्दुओं के बीच वोल्टता पात सदा बराबर होना चाहिए, इसलिए समान्तर LCR परिपथ में प्रेरक, संधारित्र और प्रतिरोधक के सिरों पर समान विभव पात होना चाहिए। इसलिए एक अकेला फेजर ε 0 , प्रत्येक अवयव के सिरों पर विभव पात दर्शाने के लिए प्रयुक्त किया जाता है। परन्तु अलग-अलग अवयवों में धाराओं के अलग-अलग आयाम और कलाएं होंगी। इसलिए I R , I L और I C , धारा फेजर दशति हैं [ चित्र 1]| फेजरों I R , I L और I C का वेक्टर जेड़, फेज़र I 0 के बराबर है जहाँ
I 0 = I R 2 + ( I C - I L ) 2
= ( ε 0 R ) 2 + ( ε 0 X C - ε 0 X L ) 2
( क्योंकि I R , ω 0 के साथ समान कला में है : I L , ε 0 से π / 2 पश्च और I C , ε 0 से π / 2 आगे है )
या I 0 = ε 0 1 R 2 + ( 1 X C - 1 X L ) 2 = ε 0 Z
जहाँ 1 Z = 1 R 2 + ( 1 X C - 1 X L ) 2 = 1 R 2 + ( ω C - 1 ω L ) 2
इस प्रकार समान्तर LCR परिपथ की प्रभावी प्रतिबाधा इस समीकरण । से प्राप्त होती है:
1 Z = 1 R 2 + ( ω C - 1 ω L ) 2
ω = ω r और 1 Z न्यूनतम है जब ω C = 1 ω L अर्थात ω = ω r = 1 L C हो।
जब ω = ω r (अर्थात अनुनाद पर ), तो कुल समांतर LCR परिपथ में धारा आयाम I rms , न्यूनतम है क्योंकि Z अधिकतम है।
I rms = ε rms R = 230 40 = 5.75 A
I rms R = ε rms R = 230 40 = 5.75 A
I rms L = ε rms ω r L = 230 50 × 5.0 = 0.92 A
I rms C = ε rms ( 1 ω r C ) = ε rms × ω r C
= 230 × 50 × ( 80 × 10 - 6 ) = 0.92 A

|
Updated on:21/07/2023
Class 12PHYSICSALTERNATING CURRENT

Topper's Solved these Questions

Similar Questions