m द्रव्यमान और a व्यासार्ध के एक पतले अचालक रिंग पर आवेश q है। यह अपने अक्ष, जो कवधिर है, के गिर्द मुक्त रूप से घूमता है। आरम्भ में रिंग, विराम अवस्था में था और कोई चुम्बकीय क्षेत्र उपस्थित नहीं था। समय पर एकसमान चुम्बकीय क्षेत्र लगा दिया जाता है जो ऊर्ध्वाधर दिशा में नीचे की ओर है [चित्र IV.35] और समय के साथ B=B0t नियम के अनुसार बढ़ता है।
![m द्रव्यमान और a व्यासार्ध के एक पतले अचालक रिंग पर आवेश q है। यह अपने अक्ष, जो कवधिर है, के गिर्द मुक्त रूप से घूमता है। आरम्भ में रिंग, विराम अवस्था में था और कोई चुम्बकीय क्षेत्र उपस्थित नहीं था। समय पर एकसमान चुम्बकीय क्षेत्र लगा दिया जाता है जो ऊर्ध्वाधर दिशा में नीचे की ओर है [चित्र IV.35] और समय के साथ B = B(0)t नियम के अनुसार बढ़ता है। रिंग से सम्बन्धित कॉलम- I में दी गई अलग-अलग राशियों को कॉलम- IIमें दिए गए उनके मानों से मिलाएँ।](https://d10lpgp6xz60nq.cloudfront.net/physics_images/GRB_SUL_HIN_PHY_XII_C10_E08_144_Q01.png)
रिंग से सम्बन्धित कॉलम- I में दी गई अलग-अलग राशियों को कॉलम- IIमें दिए गए उनके मानों से मिलाएँ।
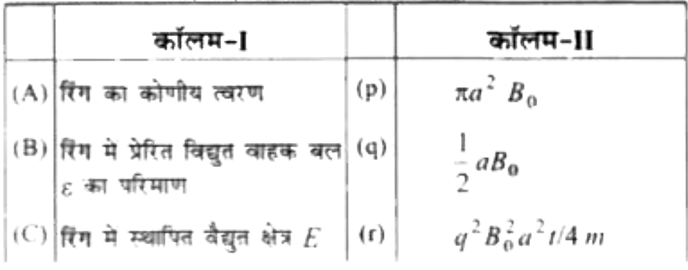

The correct Answer is:(A→s);(B→p);(C→q,t);(D→r)
(B→p) ε=dϕBdt=ddt(BA)=(πa2)(dBdt)=πa2B0
(C→q,t) वैधुत क्षेत्र E=ε2πa=12aB0
(क्योंकि अनुच्छेद 9.4 से ε=∮→E.→dl)
E स्पर्शरेखीय रूप में (tangentially) कार्य करता है।
(A→s) क्योंकि dτ=Fa=E(dq)a=12a2B0dq, इसलिए
τ=12a2B0∫dq=12a2B0q
और α=τI=12a2B0qma2=B0q2m (क्योंकि I=ma2⎞⎠
(D→r) क्योंकि ω=αt=B0qt2m, इसलिए
P=τω(12a2B0q)(B0qt2m)=q2B20a2t4m
Topper's Solved these Questions
- प्रत्यावर्ती धाराएँ BOOK - GRB PUBLICATION HINDICHAPTER - प्रत्यावर्ती धाराएँ EXERCISE - कथन-कारण-आधारित प्रश्न
15 Videos
- प्रत्यावर्ती धाराएँ BOOK - GRB PUBLICATION HINDICHAPTER - प्रत्यावर्ती धाराएँ EXERCISE - पूर्णांक उत्तर वाले प्रश्न
10 Videos
- प्रत्यावर्ती धाराएँ BOOK - GRB PUBLICATION HINDICHAPTER - प्रत्यावर्ती धाराएँ EXERCISE - पैरा-आधारित बहुविकल्पीय बोधात्मक प्रश्न पैरा 6
2 Videos
- प्रकाशिक यन्त्रBOOK - GRB PUBLICATION HINDICHAPTER - प्रकाशिक यन्त्रEXERCISE - NCERT पाठ्यपुस्तक अभ्यास
8 Videos
- विद्युत परिपथ , विद्युत ऊर्जा और शक्ति BOOK - GRB PUBLICATION HINDICHAPTER - विद्युत परिपथ , विद्युत ऊर्जा और शक्ति EXERCISE - प्रतियोगिता सामग्री ( रिक्त स्थान भरना )
15 Videos
Similar Questions
A: श्रेणीक्रम LCR परिपथ में अनुनाद हो सकता है।
R: अनुनाद होता है यदि प्रेरणिक (inductive) और धारिता प्रतिघात, समान और विपरीत हों।
View Solutionयदि 0.1mलम्बाई वाले चालक को 0.2Ω प्रतिरोध के लूप पर (जो 1Wb/m2 के चुंबकीय क्षेत्र पर लम्बवत है ) चलाने के लिए आवश्यक शक्ति 0.05W हो, तो चालक का वेग (m/s में)...........है।
View Solutionएक ऊष्मीय शक्ति संयंत्र 4000 V पर 600 kW वैद्युत शक्ति उत्पन्न करता है जिसे खपतकारों के प्रयोग के लिए शक्ति संयंत्र से 20 km दूर स्थान तक ले जाया जाना है इसे या तो अधिक धारा-वहन क्षमता वाली केबल से सीधा ले जाया जा सकता है या दोनों सिरों पर उच्चायी तथा अपचायी ट्रांसफार्मरों के संयोजन के प्रयोग से। सोधे संचरण से काफी ऊर्जा क्षयित होती है। ट्रांसफार्मरों के प्रयोग में क्षय काफ़ी कम होता है। इस ढंग में संयंत्र के पार्श्व में उच्चायी ट्रांसफार्मर प्रयुक्त किया जाता है ताकि धारा कम हो जाए। खपतकारों के पास अपचायी ट्रांसफार्मर प्रयुक्त किया जाता है ताकि उन्हें निर्धारित निम्न वोल्टता पर शक्ति सप्लाई की जा सके। यह कल्पना करना संगत है कि शक्ति केबल पूर्णतया प्रतिरोधक है और ट्रांसफार्मर, जो एक इकाई शक्ति घटक वाले हैं, आदर्श है। वर्णित सभी धाराएँ और वोल्टताएँ वर्ग माध्य मूल मान हैं।
उपरोक्त के आधार पर निम्न प्रश्नों के सबसे उचित विकल्प चुने :
यदि 0.4Ω/km वाले केवल प्रतिरोध से संचरण हंग का प्रयोग किया जाए, तो संचरण के दौरान क्षषित शक्ति (% में) हैं :
View Solutionएक छोटे दूरदर्शक के अभिदृश्यक लेन्स की फोकस दुरी 144cm , और नेत्रिका की 6.0cm है। दूरदर्शक की आवर्धन क्षमता क्या है ? अभिदृश्यक और नेत्रिका के बीच कितनी दुरी है ?
View Solutionएक H-परमाणु में एक इलेक्ट्रॉन नाभिक के इर्द-गिर्द 6.6×1015 rps लगाता है। तुल्य धारा ..............A है।
View Solutionकोई रेखा x-अक्ष और y-से साथ क्रमशः 60∘ तथा 45∘ के कोण बनाती है। इनके द्वारा घनत्व दिशा में z-अक्ष के साथ कितना कोण बनेगा ?
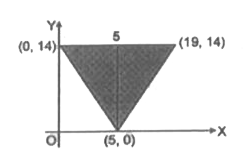
View Solutionचित्र में दिखाए गए छायांकित क्षेत्र के लिए असामिका है-
View Solutionएकसमान चुम्बकीय क्षेत्र में आवेश की गति
View Solutionटोरोइड के कारण चुम्बकीय क्षेत्र | एक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल
View Solutionएक व्यक्ति पश्चिम दिशा की ओर मूँह करके खड़ा है | वह दक्षिणावर्त दिशा में 45∘ के कोण पर घूमता है फिर वह पुनः उसी दिशा में 180∘ के कोण पर घूमता है और फिर वह वामावर्त दिशा में 270∘ के कोण पर घूमता है | अब वह किस दिशा की ओर खड़ा है ?
View SolutionMgCO3 के 10g को गर्म करने पर, यह 0.1 मोल CO2 और 4gmgO में अपघटित हो जाता है। MgCO3 की प्रतिशत शुद्धता होगी : (दिया गया है, Mg,C और O के परमाणु भार क्रमशः 24,12 और 16 u है)
View Solutionएक द्रव, जल में अमिश्रणीय है जो कि 0.983 atm के दाब और 95.2^(@)C पर भाप आसवित है। आसुत में जल के प्रति ग्राम में उपस्थित द्रव का द्रव्यमान क्या है। द्रव का मोलर द्रव्यमान 134.3 g/mol है और जल का वाष्प दाब 0.84 atm है। साथ ही, शुद्ध द्रव का वाष्प दाब 0.143 atm है।
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionएक धातु वायु के आधिक्य में दहन करने पर X निर्मित करती है। जल के साथ जल अपघटन पर X,H_(2)O_(2) और O_(2) के साथ एक और उत्पाद निर्मित करता है। धातु कौन सी है?
View Solutionसंकुल जो प्रतिबिंब समावयवियों के एक युग्म के रूप में विद्यमान है, वह है
View Solutionएक आदर्श गैस के दस मोलों को एक बंद पात्र में भरा जाता है । पात्र में बेलन और पिस्टन के प्रकार की व्यवस्था है और 0.821 atm पर गैस का दाब स्थिर रहता है। निम्नलिखित में से कौन सा आलेख logV और logT के परिवर्तन का सही निरूपण करता है? (V= आयतन(लीटर में) और T= ताप (केलिवन में)
View Solution
