भाजकता का नियम यह निर्धारित करने की एक विधि है कि क्या दी गयी संख्या एक निश्चित भाजक (divisor) द्वारा विभाज्य (divisible) है या नहीं
हमारे पास 2, 3, 4, 5, 6, 7, 8, 9, 10 और 11 के लिए विभाज्यता नियम हैं।
2 के लिए विभाज्यता परीक्षण :
यदि किसी संख्या के इकाई का अंक 0,2,4,6 या 8 है, तो वह संख्या 2 से विभाज्य होती है।
उदाहरण:
12, 34, 56 और 78
3 के लिए विभाज्यता परीक्षण :
एक संख्या 3 से विभाज्य है, यदि उसके अंकों का योग 3 से विभाज्य है
उदाहरण:
27
क्योकि
2+7=9
जो की 3 से विभाज्य हैं
अत: 27, 3 से विभाज्य है
4 के लिए विभाज्यता परीक्षण :
कोई संख्या 4 से विभाज्य होती है यदि उसके अंतिम दो अंकों (अर्थात इकाई और दहाई) से बनी संख्या 4 से विभाज्य हो
उदाहरण:
1396, 4 से विभाज्य है क्योंकि इसके अंतिम दो अंक यानी 96, 4 से विभाज्य है।
5 के लिए विभाज्यता परीक्षण :
यदि किसी संख्या का इकाई का अंक 5 या 0 है, तो वह 5 से विभाज्य है।
उदाहरण:
75, 90, 100 और 125
6 के लिए विभाज्यता परीक्षण :
यदि कोई संख्या 2 और 3 दोनों से विभाज्य है, तो वह 6 से भी विभाज्य है।
उदाहरण:
120,
चुकि 120, 2 और 3 से विभाज्य है। इसलिए, यह 6 से भी विभाज्य है
7 के लिए विभाज्यता परीक्षण :
कोई संख्या 7 से विभाजित होगी यदि जब संख्या के इकाई के अंक को दुगुना करे तथा इसे शेष अंकों से बनी संख्या से घटाया जाए यदि प्राप्त संख्या 7 से विभाजित है तो वह पूरी संख्या भी 7 से विभाजित होगी
NOTE= यह नियम 1 से अधिक बार भी प्रयोग किया जा सकता है ।
उदाहरण :1 = 3541
step1
इकाई का अंक =1
step2 दुगुना = 1×2=2
step3 शेष संख्या = 354−2
=352
step4 प्राप्त संख्या 352 , 7 से विभाजित नहीं है अतः यह पूरी संख्या भी 7 से विभाजित नहीं होगी ।
इसी प्रकार इस नियम को फिर से प्रयोग करने पर भी यह संख्या 7 से विभाजित नहीं होगी ।
उदाहरण :2
826
क्योंकि
82−(6×2)
=82−12
=70,
यहा प्राप्त संख्या 70,
7 से विभाजित है अतः यह पूरी संख्या भी 7 से विभाजित होगी ।
8 के लिए विभाज्यता परीक्षण :
कोई संख्या 8 से विभाज्य होती है, यदि उसके अंतिम तीन अंकों से बनी संख्या 8 से विभाज्य हो।
उदाहरण:
73512, 8 से विभाज्य है क्योंकि इसके अंतिम तीन अंक यानी 512, 8 से विभाज्य हैं।
9 के लिए विभाज्यता परीक्षण :
एक संख्या 9 से विभाज्य होती है यदि उसके अंकों का योग 9 के द्वारा विभाज्य है
उदाहरण:
126
इसके अंकों का योग = 1+2+6=9,
जो 9 से विभाज्य है।
अत: 126, 9 से विभाज्य है।
10 के लिए विभाज्यता परीक्षण :
यदि किसी संख्या का इकाई का अंक 0 है, तो वह 10 से विभाज्य है।
उदाहरण:
90, 100
11 के लिए विभाज्यता परीक्षण :
किसी संख्या के विषम स्थानों (दाईं ओर से) के अंकों के योग और सम स्थानों (दाईं ओर से) के अंकों के योग के बीच अंतर ज्ञात कीजिए यदि अंतर या तो 0 है या 11 से विभाज्य है, तो संख्या 11 से विभाज्य है।
उदाहरण =
1234321, 11 से विभाज्य है,
क्योंकि
(1+3+3+1)−(2+4+2)
=8−8
=0
जो 11 से विभाज्य है।
कुछ और विभाज्यता नियम
(1) मान लीजिए a और b दो दी गई संख्याएं हैं। यदि a, b से विभाज्य है तो यह b के सभी गुणनखंडों से भी विभाज्य होगा।
उदाहरण
यदि 24, 12 से विभाज्य है, तो 24, 12 के सभी गुणनखंडों (अर्थात 2, 3, 4, 6) से भी विभाज्य होगा।
(2) मान लीजिए a और b दो सह-अभाज्य संख्याएँ हैं। यदि c, a और b से विभाज्य है तो c, a और b के गुणनफल से विभाज्य होगा
उदाहरण
यदि 24, 2 और 3 से विभाज्य है जो सह-अभाज्य संख्याएँ हैं तो 24 भी 2 और 3 (2×3=6) के गुणनफल से विभाज्य होगा।
(3) यदि a और b, c से विभाज्य हैं तो (a+b) भी c से विभाज्य होगा।
उदाहरण
यदि 24 और 12, 4 से विभाज्य हैं तो (24+12)=36 भी 4 से विभाज्य होंगे।
(4) यदि a और b, c से विभाज्य हैं तो a−b भी c से विभाज्य होंगे।
उदाहरण
यदि 24 और 12, 4 से विभाज्य हैं तो 24−12=12 भी 4 से विभाज्य होगा।
यदि किसी संख्या के इकाई का अंक 0,2,4,6 या 8 है, तो वह संख्या 2 से विभाज्य होती है।
उदाहरण:
12, 34, 56 और 78
एक संख्या 3 से विभाज्य है, यदि उसके अंकों का योग 3 से विभाज्य है
उदाहरण:
27
क्योकि
2+7=9
जो की 3 से विभाज्य हैं
अत: 27, 3 से विभाज्य है
कोई संख्या 4 से विभाज्य होती है यदि उसके अंतिम दो अंकों (अर्थात इकाई और दहाई) से बनी संख्या 4 से विभाज्य हो
उदाहरण:
1396, 4 से विभाज्य है क्योंकि इसके अंतिम दो अंक यानी 96, 4 से विभाज्य है।
यदि किसी संख्या का इकाई का अंक 5 या 0 है, तो वह 5 से विभाज्य है।
उदाहरण:
75, 90, 100 और 125
यदि कोई संख्या 2 और 3 दोनों से विभाज्य है, तो वह 6 से भी विभाज्य है।
उदाहरण:
120,
चुकि 120, 2 और 3 से विभाज्य है। इसलिए, यह 6 से भी विभाज्य है
कोई संख्या 7 से विभाजित होगी यदि जब संख्या के इकाई के अंक को दुगुना करे तथा इसे शेष अंकों से बनी संख्या से घटाया जाए यदि प्राप्त संख्या 7 से विभाजित है तो वह पूरी संख्या भी 7 से विभाजित होगी
NOTE= यह नियम 1 से अधिक बार भी प्रयोग किया जा सकता है ।
उदाहरण :1 = 3541
step1 इकाई का अंक =1
step2 दुगुना = 1×2=2
step3 शेष संख्या = 354−2
=352
step4 प्राप्त संख्या 352 , 7 से विभाजित नहीं है अतः यह पूरी संख्या भी 7 से विभाजित नहीं होगी ।
इसी प्रकार इस नियम को फिर से प्रयोग करने पर भी यह संख्या 7 से विभाजित नहीं होगी ।
उदाहरण :2
826
क्योंकि
82−(6×2)
=82−12
=70,
यहा प्राप्त संख्या 70, 7 से विभाजित है अतः यह पूरी संख्या भी 7 से विभाजित होगी ।
कोई संख्या 8 से विभाज्य होती है, यदि उसके अंतिम तीन अंकों से बनी संख्या 8 से विभाज्य हो।
उदाहरण:
73512, 8 से विभाज्य है क्योंकि इसके अंतिम तीन अंक यानी 512, 8 से विभाज्य हैं।
एक संख्या 9 से विभाज्य होती है यदि उसके अंकों का योग 9 के द्वारा विभाज्य है
उदाहरण:
126
इसके अंकों का योग = 1+2+6=9,
जो 9 से विभाज्य है।
अत: 126, 9 से विभाज्य है।
यदि किसी संख्या का इकाई का अंक 0 है, तो वह 10 से विभाज्य है।
उदाहरण:
90, 100
किसी संख्या के विषम स्थानों (दाईं ओर से) के अंकों के योग और सम स्थानों (दाईं ओर से) के अंकों के योग के बीच अंतर ज्ञात कीजिए यदि अंतर या तो 0 है या 11 से विभाज्य है, तो संख्या 11 से विभाज्य है।
उदाहरण =
1234321, 11 से विभाज्य है,
क्योंकि
(1+3+3+1)−(2+4+2)
=8−8
=0
जो 11 से विभाज्य है।
दी गई संख्या 7 से विभाजित होगी यदि जब संख्या के इकाई के अंक को दुगुना करे तथा इसे शेष अंकों से बनी संख्या से घटाया जाए यदि प्राप्त संख्या 7 से विभाजित है तो वह पूरी संख्या भी 7 से विभाजित होगी
NOTE= यह नियम 1 से अधिक बार भी प्रयोग किया जा सकता है ।
उदाहरण = 3541
step1
इकाई का अंक =1
step2 दुगुना = 1×2=2
step3 शेष संख्या = 354−2
=352
step4 अतः प्राप्त संख्या 352 , 7 से विभाजित नहीं है ।
इसी प्रकार इस नियम को फिर से प्रयोग करने पर भी यह संख्या 7 से विभाजित नहीं होगी ।
Topper's Solved these Questions
- चतुर्भुजों को समझना BOOK - NCERT HINDICHAPTER - चतुर्भुजों को समझना EXERCISE - प्रयास कीजिए
3 Videos
- चतुर्भुजों को समझना BOOK - NCERT HINDICHAPTER - चतुर्भुजों को समझना EXERCISE - प्रश्नावली 3.1
7 Videos
- घातांक और घातBOOK - NCERT HINDICHAPTER - घातांक और घातEXERCISE - प्रयास कीजिए
5 Videos
- ठोस आकारों का चित्रण BOOK - NCERT HINDICHAPTER - ठोस आकारों का चित्रण EXERCISE - प्रश्नावली 10.3
8 Videos
Similar Questions
एक सम षड्भुज लीजिए ( आकृति 3.10 ) |
(i) बाह्य कोणों x, y , z, p, q तथा r की मापों का योग क्या है ?
(ii) क्या x = y = z = p = q = r है ? क्यों ?
(iii) प्रत्येक की माप क्या है ?
(i) बाह्य कोण
(ii) अंतः कोण
(iv) इस क्रियाकलाप को निम्नलिखित के लिए दोहराएँ
(i) एक सम अष्टभुज
(ii) एक सम 20 भुज

View Solutionयहाँ पर कुछ आकृतियाँ दी गई हैं :
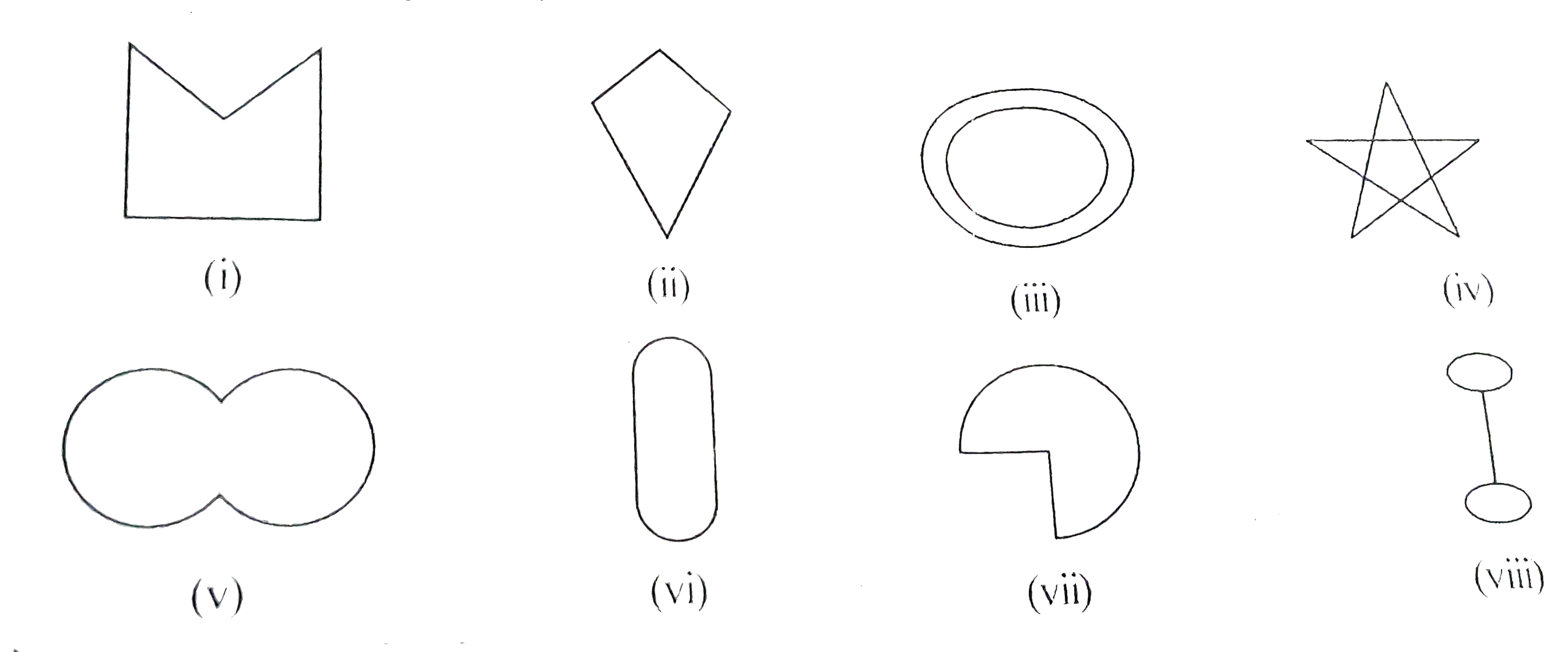
प्रत्येक का वर्गीकरण निम्नलिखित आधार पर कीजिए :
(a) साधारण वक्र
(b) साधारण बंद वक्र
(c) बहुभुज
(d) उत्तल बहुभुज
(e) अवतल बहुभुज
View Solutionगुणात्मक प्रतिलोम लिखिए
(i) 2−4 (ii) 10−5 (iii) 7−2 (iv) 5−3 (v) 10−100
View Solutionक्या किसी बहुफलक के फलक नीचे दिए अनुसार हो सकते हैं?
(i) 3 त्रिभुज (ii) 4 त्रिभुज (iii) एक वर्ग और चार त्रिभुज
View Solutionनीचे दर्शाये दशमलव प्रसार के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नही। यदि यह परिमेय संख्या है, तो इसके हर के अभाज्य गुणनखंडन के बारे में अपनी टिप्पणी लिखिए-
27.¯¯¯¯¯¯¯¯¯¯¯¯143857
View Solutionकुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि परिमेय संख्या है pq और के रूप की है तो q के अभाज्य गुणनखंडों के बारे में आप क्या कह सकते हैं?
58.567823
View Solutionकुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि परिमेय संख्या है pq और के रूप की है तो q के अभाज्य गुणनखंडों के बारे में आप क्या कह सकते हैं?
0.00352
View Solutionकुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि परिमेय संख्या है pq और के रूप की है तो q के अभाज्य गुणनखंडों के बारे में आप क्या कह सकते हैं?
15.712121212.....
View Solutionकुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि परिमेय संख्या है pq और के रूप की है तो q के अभाज्य गुणनखंडों के बारे में आप क्या कह सकते हैं?
8.652365236523
View Solutionकुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि परिमेय संख्या है pq और के रूप की है तो q के अभाज्य गुणनखंडों के बारे में आप क्या कह सकते हैं?
0.54
View Solutionकुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि परिमेय संख्या है pq और के रूप की है तो q के अभाज्य गुणनखंडों के बारे में आप क्या कह सकते हैं?
0.00026
View Solutionसंख्या 6 का "9 के पूरक" ........." है।
View Solutionयदि 4964A, 9 से विभाज्य है तो अंक A का मान क्या हो सकता है?
View Solutionयदि संख्या 354Y2, 6 का एक गुणज है तो Yअंक का मान क्या हो सकता है?
View Solutionदो अंको की एक संख्या में इकाई स्थान का अंक दहाई स्थान के अंक से 3 अधिक है यदि दोनों अंकों का जोड़ 11 हो तो संख्या निकालिए।
View Solutionप्रोटॉन का परीक्षण #!#वसा का परीक्षण #!#विभिन्न पोषक हमारे हमारे शरीर के लिए क्या करते है ?
View Solution
