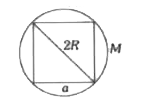
किसी ठोस गोले का द्रव्यमान M तथा इसकी त्रिज्या R है। इसमें से अधिकतम सम्भव आयतन का एक क्यूब (धन) काट लिया जाता है। इस क्यूब का जड़त्व आघूर्ण कितना होगा, यदि इसका घूर्णन अक्ष इसके केन्द्र से होकर गुजरता है तथा इसके किसी एक फलक के लम्बवत् है।
MR232√2π
MR216√2π
4MR29√3π
4MR23√3π
The correct Answer is:C
दिया गया चित्र म द्रव्यमान के एक ठोस गोले को darshata है गोले की त्रिज्या R है गोले का आयतन =
V=4π3R3है
गोले का घनत्व है ρ=MV=M4π3R3=3M4πR3
इस ठोस गोले से अधिकतम संभव आयतन एक घनाकर लिया गया है
अतः 2R=√2a, जहाँ a अधिकतम आयतन के धन के एक फलक की लम्बाई a=2R√3
धन का द्रव्यमान M.=ρa3=3M4πR38R33√3=2M√3π
धन का जड़त्व आघूर्ण है
Ma26=2M√3π×16×(2R√3)2=8MR218√3π=4MR29√3π.
Topper's Solved these Questions
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - बल आघूर्ण तथा बलयुग्म
35 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - कोणीय संवेग
57 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - कोणीय विस्थापन, वेग तथा त्वरण
22 Videos
- घर्षण BOOK - ERRORLESS HINDICHAPTER - घर्षण EXERCISE - SELF EVALUATION TEST
11 Videos
- चुम्बकत्व BOOK - ERRORLESS HINDICHAPTER - चुम्बकत्व EXERCISE - Self Evaluation Test
15 Videos
Similar Questions
माना कि किसी कण, जिसका स्थित सदिश →r है, पर लगने वाला बल →F है, एवं मूल बिन्दु के परितः इस बल का बल आघूर्ण →T है
View Solutionसौर मण्डल में उपग्रहों की गति किसका उदाहरण है
View Solutionएक रस्सी को पहिये की परिधि पर लपेटा गया है। जिसकी त्रिज्या है, पहिये का अक्ष क्षैतिज है, एवं जडत्व आघूर्ण I है। रस्सी के सिरे पर mg भार लगाया गया है और विराम अवस्था से नीचे गिराया जाता है h दूरी से गिरने के पश्चात् पहिये का कोणीय वेग होगा
View Solutionयदि 19.6 न्यूटन का बल किसी 10 किग्रा के पिण्ड पर लगया जाता है तल के समांतर इस पिण्ड 5 किग्रा का द्रिव्यमान रख दिया जाए तो सतह के समांतर संयुक्त वस्तु को गति करने के लिए आरोपित बल का मान होगा
View Solutionएक नाल चुंबक (अर्धवृत्ताकार), चुंबक के ध्रुवो के बीच की दूरी 0.1m है एव ध्रुव सामर्थ्य 0.01 amp-m है । ध्रुवो के बीच में मध्य बिंदु पर चुंबकीय प्रेरण होगा

View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionवह समतल, जो बिन्दुओ (−3,−3,4) तथा (3,7,6) को मिलाने वाले रेखाखण्ड का लंबसमद्विभाजक करता है, निम्न में से किस एक बिंदु से होकर जाता है?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि z−αz+α(α∈R) एक शुद्ध रूप से काल्पनिक संख्या है तथा |z|=2 है तो α का एक मान है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionयदि बिन्दु P(−3,4) से होकर जाने वाली एक सरल रेखा इस प्रकार है कि इसके निर्देशांक अक्षो के बीच अंत: खंडित भाग का मध्य -बिन्दु P है, तो इसका समीकरण है
View Solutionमाना एक दीर्घवृत्त कि नाभियां S तथा S' है तथा इसके लघु अक्ष का कोई एक शीर्ष B है। यदि ΔS'BS एक समकोण त्रिभुज है जिसका समकोण B पर है तथा ΔS'BS का क्षेत्रफल 8 वर्ग इकाई है, तो दीर्घवृत्त की एक नाभिलम्ब जीवा की लम्बाई है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solution
