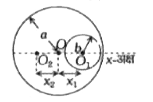
सेमी त्रिज्या की चकती से एक 2 सेमी त्रिज्या की चकत्ती को इस प्रकार निकालते हैं कि केन्द्रों के बीच की दूरी 3.2 सेमी रहे तो चकती का द्रव्यमान केन्द्र विस्थापित होगा
0.4 सेमी
2.4 सेमी
1.8 सेमी
1.2 सेमी
The correct Answer is:A
माना बड़ी चकती की त्रिज्या a तथा छोटी चकती की त्रिज्या b है और द्रव्यमान केंद्र अपनी प्रारंभिक स्थिति से x2 दुरी विस्थापित होकर बिंदु O2 पर पहुँचता जाता है।
इसलिए नए द्रव्यमान की स्थिति
XCM=−σπb2x1σπa2−σib2
यहाँ पर a=6cm,b=2cm,x1=3.2cm
इसलिये XCM=−σ×π(2)2×3.2σ×π×(6)2−σ×π×(2)2
=12.8π32π=−0.4cm.
Topper's Solved these Questions
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - GRAPHICAL QUESTIONS
6 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - JEE SECTION
36 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - नत समतल पर घूर्ण
21 Videos
- घर्षण BOOK - ERRORLESS HINDICHAPTER - घर्षण EXERCISE - SELF EVALUATION TEST
11 Videos
- चुम्बकत्व BOOK - ERRORLESS HINDICHAPTER - चुम्बकत्व EXERCISE - Self Evaluation Test
15 Videos
Similar Questions
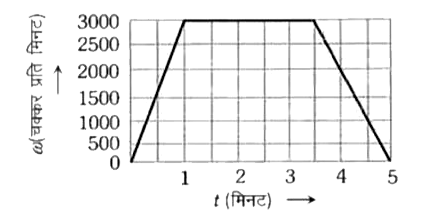
एक जेट इंजन के परीक्षण के दौरान, उसका संपीडक (Compressor) निम्न ग्राफ के अनुसार चक्रण करता है। परीक्षण के दौरान संपीडक द्वारा पूर्ण किये गये चक्करों की संख्या होगी
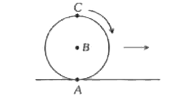
View Solutionएक स्थिर क्षैतिज समतल पृष्ठ पर एक गोला बिना फिसले लुढ़क रहा है। चित्र में, A तल से सम्पर्क बिन्दु, B गोले का केन्द्र तथा C उसका सबसे ऊपरी बिन्दु है, तब
View Solutionएक गोला θ नति वाले नत समतल पर नीचे की ओर लुढ़क रहा है। तली पर पहुंचने पर गोले का त्वरण होगा
View Solutionयदि 19.6 न्यूटन का बल किसी 10 किग्रा के पिण्ड पर लगया जाता है तल के समांतर इस पिण्ड 5 किग्रा का द्रिव्यमान रख दिया जाए तो सतह के समांतर संयुक्त वस्तु को गति करने के लिए आरोपित बल का मान होगा
View Solutionएक नाल चुंबक (अर्धवृत्ताकार), चुंबक के ध्रुवो के बीच की दूरी 0.1m है एव ध्रुव सामर्थ्य 0.01 amp-m है । ध्रुवो के बीच में मध्य बिंदु पर चुंबकीय प्रेरण होगा

View Solutionएक दीर्घवृत्त एक धागे से निर्मित किया जाता है, जिसके सिरों को दो पिनों द्वारा स्थिर बिंदुओं S और S' से बाँध दिया है। अब एक पेन्सिल की नोंक से धागे को तानकर उसे कागज पर इस प्रकार चलाया की धागा तना रहे। यदि इस प्रकार बने दीर्घवृत्त के अक्ष क्रमशः 6 सेमी तथा 4 सेमी हों, तो धागे की लम्बाई और पिनों के बीच की दूरी ज्ञात कीजिए।
View Solutionएक 3.1 सेमी त्रिज्या में एक 2.3 सेमी की जीवा काटिए और उसके दोनों सिरों पर स्पर्श रेखाएं खींचिए।
View Solutionएक 3.2 सेमी त्रिज्या का वृत्त खींचिए। उस पर दो स्पर्श रेखाएं इस प्रकार खींचिए की वो परस्पर 70∘ का कोण बनाती हो।
View Solutionएक वृत्त 3 सेमी त्रिज्या को खींचिए। जिसके केंद्र O से 5 सेमी दूरी स्थित P से दो स्पर्श रेखाओ की रचना कीजिए।
View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View SolutionThe sides of a triangle are 24cm,45cm and 51cm. At each of its vertices, circles of radius 10.5cm are drawn. What is the area of the triangle, excluding the portion covered by sectors of the circles? ( π=227)
एक त्रिभुज की भुजाएं 24 सेमी, 45 सेमी तथा 51 सेमी की हैं | इसके प्रत्येक शीर्ष पर 10.5 सेमी त्रिज्या वाले वृत्त खींचे जाते हैं | वृत्त के खंडो द्वारा घेरे गए भाग को छोड़ कर इस त्रिभुज का क्षेत्रफल क्या होगा ?
View SolutionWhat is the distance between two parallel tangents of a circle of radius 8 cm?
8 सेमी त्रिज्या वाले वृत्त की दो समानांतर स्पर्श रेखाओं के बीच की दूरी कितनी है?
View SolutionTwo circles touch each other externally. The distance between their centres is 8 cm. If the radius of one circle is 3 cm, then the radius of the other circle is: दो वृत्त एक दूसरे को बाह्य रूप से स्पर्श करते हैं। उनके केंद्रों के बीच की दूरी 8 सेमी है। यदि एक वृत्त की त्रिज्या 3 सेमी है, तो दूसरे वृत्त की त्रिज्या है:
View Solution
