निश्चित ताप पर अभिक्रिया की मानक गिब्स ऊर्जा (ΔrG∘) का परिकलन ΔrG∘=ΔrH∘−T.ΔrS∘ से कर सकते है तथा अभिक्रिया के लिए तापमान के साथ ΔrH∘ तथा ΔrS∘ के मान में परिवर्तन को निम्न प्रकार परिकलित किया जा सकता है
ΔrH∘T2−ΔrH∘T1=ΔrC∘p(T2−T1)
ΔrS∘T1−ΔrS∘T1=ΔrC∘pln(T2T1)
ΔrG∘=ΔrH∘−TΔrS∘
ΔrG∘=−RTlnKeq द्वारा
निम्न अभिक्रिया पर विचार करें
CO(g)+2H2(g)⇔CH3OH(g)
दिया है :ΔfH∘(CO,g)=−114kJ/mole
S∘(CH3OH,g)=240J/K mol,C∘p,m(H2,g)=29JK−1mol−1
S∘(CO,g)=198J/mol−K,C∘p,m(H2)=28.8 J/mole - K
C∘p,m(CO)=29.4J/mol - K , C∘p,m(CH3OH)=44J/mol-K
तथा ln(320300)=0.06 , सभी आँकड़े 300K पर है।
320K ताप पर ΔrS∘ है
155.18J/mol-K
150.02 J/mol- K
172J/mol-K
इनमें से कोई नहीं
The correct Answer is:D
320K पर DetlarS∘=ΔrS∘320
∵ΔrS∘320−ΔrS∘300=ΔrC∘Pln(T2T1)
जहाँ ΔrC∘P=44−29.4−2×28.8<br>=−43JKmol<br> therefore Delta_r S_(320)^@ =-43ln (320/300) + (-16)
= -18.74 J/K mol
Topper's Solved these Questions
- उष्मागतिकी तथा उष्मारसायन BOOK - ERRORLESS HINDICHAPTER - उष्मागतिकी तथा उष्मारसायन EXERCISE - JEE ADVANCED (INTEGER TYPE QUESTIONS)
6 Videos
- उष्मागतिकी तथा उष्मारसायन BOOK - ERRORLESS HINDICHAPTER - उष्मागतिकी तथा उष्मारसायन EXERCISE - JEE ADVANCED (MATRIX MATCH TYPE QUESTIONS)
4 Videos
- उष्मागतिकी तथा उष्मारसायन BOOK - ERRORLESS HINDICHAPTER - उष्मागतिकी तथा उष्मारसायन EXERCISE - JEE ADVANCED (REASONING TYPE QUESTIONS)
4 Videos
- उपसहसंयोजक रसायनBOOK - ERRORLESS HINDICHAPTER - उपसहसंयोजक रसायनEXERCISE - ASSERTION AND REASON
10 Videos
- एल्कोहल , फिनॉल एवं ईथर BOOK - ERRORLESS HINDICHAPTER - एल्कोहल , फिनॉल एवं ईथर EXERCISE - ASSERTION & REASON
30 Videos
Similar Questions
स्थिर आयतन कैलोरीमापी (constant volume calorimeter) में एक गैस 'X' (अणुभार = 28) के 3.5g ग्राम को ऑक्सीजन की अधिकता में 298.0K पर दहन किया जाता है। इस दहन के फलस्वरूप कैलोरीमापी का तापमान 298.0K से बढ़कर 298.45K हो जाता है। यदि कैलोरीमापी की ऊष्माधारिता (heat capacity) का मान 2.5kJK−1 है, तो गैस 'x' की दहन ऊष्मा (enthalpy of combustion) का सांख्यिक मान (numerical value) kJmol−1 में है
View Solutionइस खण्ड में कुछ प्रश्न है। प्रत्येक प्रश्न में कॉलम-I में कुछ कथन (A, B, C और D) और कॉलम-II में कुछ कथन (p, q, r, s और t) है। कॉलम-1 का कोई भी कथन कॉलम-II के एक कथन या एक से अधिक कथनों से मेल खाता है। उदाहरण के लिए, दिए हुए प्रश्न में यदि कथन B कथनों q और r से मेल खाता है, तो ORS में उस प्रश्न के लिये कथन B के सामने q और r से संबंधित बुलबुलों को काला कीजिए।
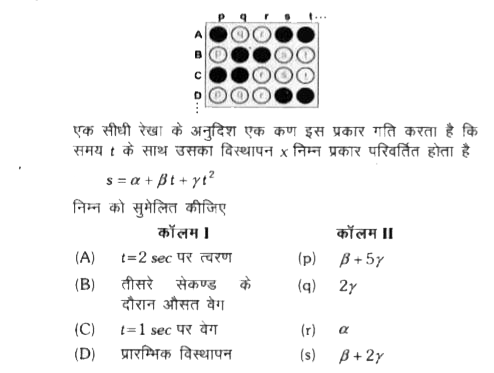
View Solutionकथन 1: साम्य पर प्रत्येक रासायनिक अभिक्रिया के लिये, अभिक्रिया की मानक गिब्स ऊर्जा शून्य होती है।
कथन 2: स्थिर दाब और ताप पर गिब्स ऊर्जा के कम होने की दिशा में रासायनिक अभिक्रिया स्वतः होती है।
View Solutionप्रक्कथन : NF3,N(CH3)3 से दुर्बल लिगेण्ड है।
कारण : NF3जलीय विलयन में आयनीकृत होकर F− आयन देता है।
View Solutionप्रक्कथन : ग्लिसरॉल एवं पामिटिक अम्ल का ट्राईएस्टर जलीय NaOH के साथ उबालने पर ठोस केक देता है जिसमें साबुन का स्पर्श होता है।
कारण : ग्लिसरॉल मुक्त होता है जो कि ग्रीस जैसा ठोस है।
View Solutionदिया गया है, C(graphite)+O2(g)→CO2(g)△r(g)Ho=−393.5kJmoI−1H2(g)+12O2(g)→H2O(l)△rHo=−285.8kJmoI−1CO2(g)=2H2O(l)→CH4(g)+202(g)△rHo=+890.3kJmoI−1 ऊपर दिए गए ऊष्मरासायनिक समीकरणों के आधार पर,298 K पर अभिक्रिया C(graphite)+2H2(g)→CH4(g)के लिए △rHo का मान होगा :
View Solutionनिश्चित ताप पर अभिक्रिया की मानक गिब्स ऊर्जा (ΔrG∘) का परिकलन ΔrG∘=ΔrH∘−T.ΔrS∘ से कर सकते है तथा अभिक्रिया के लिए तापमान के साथ ΔrH∘ तथा ΔrS∘ के मान में परिवर्तन को निम्न प्रकार परिकलित किया जा सकता है
ΔrH∘T2−ΔrH∘T1=ΔrC∘p(T2−T1)
ΔrS∘T1−ΔrS∘T1=ΔrC∘pln(T2T1)
ΔrG∘=ΔrH∘−TΔrS∘
ΔrG∘=−RTlnKeq द्वारा
निम्न अभिक्रिया पर विचार करें
CO(g)+2H2(g)⇔CH3OH(g)
दिया है :ΔfH∘(CO,g)=−114kJ/mole
S∘(CH3OH,g)=240J/K mol,C∘p,m(H2,g)=29JK−1mol−1
S∘(CO,g)=198J/mol−K,C∘p,m(H2)=28.8 J/mole - K
C∘p,m(CO)=29.4J/mol - K , C∘p,m(CH3OH)=44J/mol-K
तथा ln(320300)=0.06 , सभी आँकड़े 300K पर है।
300K ताप पर अभिक्रिया के लिए ΔrS∘ है
View Solutionनिश्चित ताप पर अभिक्रिया की मानक गिब्स ऊर्जा (ΔrG∘) का परिकलन ΔrG∘=ΔrH∘−T.ΔrS∘ से कर सकते है तथा अभिक्रिया के लिए तापमान के साथ ΔrH∘ तथा ΔrS∘ के मान में परिवर्तन को निम्न प्रकार परिकलित किया जा सकता है
ΔrH∘T2−ΔrH∘T1=ΔrC∘p(T2−T1)
ΔrS∘T1−ΔrS∘T1=ΔrC∘pln(T2T1)
ΔrG∘=ΔrH∘−TΔrS∘
ΔrG∘=−RTlnKeq द्वारा
निम्न अभिक्रिया पर विचार करें
CO(g)+2H2(g)⇔CH3OH(g)
दिया है :ΔfH∘(CO,g)=−114kJ/mole
S∘(CH3OH,g)=240J/K mol,C∘p,m(H2,g)=29JK−1mol−1
S∘(CO,g)=198J/mol−K,C∘p,m(H2)=28.8 J/mole - K
C∘p,m(CO)=29.4J/mol - K , C∘p,m(CH3OH)=44J/mol-K
तथा ln(320300)=0.06 , सभी आँकड़े 300K पर है।
320K ताप पर ΔrH∘ है
View Solutionनिश्चित ताप पर अभिक्रिया की मानक गिब्स ऊर्जा (ΔrG∘) का परिकलन ΔrG∘=ΔrH∘−T.ΔrS∘ से कर सकते है तथा अभिक्रिया के लिए तापमान के साथ ΔrH∘ तथा ΔrS∘ के मान में परिवर्तन को निम्न प्रकार परिकलित किया जा सकता है
ΔrH∘T2−ΔrH∘T1=ΔrC∘p(T2−T1)
ΔrS∘T1−ΔrS∘T1=ΔrC∘pln(T2T1)
ΔrG∘=ΔrH∘−TΔrS∘
ΔrG∘=−RTlnKeq द्वारा
निम्न अभिक्रिया पर विचार करें
CO(g)+2H2(g)⇔CH3OH(g)
दिया है :ΔfH∘(CO,g)=−114kJ/mole
S∘(CH3OH,g)=240J/K mol,C∘p,m(H2,g)=29JK−1mol−1
S∘(CO,g)=198J/mol−K,C∘p,m(H2)=28.8 J/mole - K
C∘p,m(CO)=29.4J/mol - K , C∘p,m(CH3OH)=44J/mol-K
तथा ln(320300)=0.06 , सभी आँकड़े 300K पर है।
320K ताप पर ΔrH∘ है
View Solutionनिश्चित ताप पर अभिक्रिया की मानक गिब्स ऊर्जा (ΔrG∘) का परिकलन ΔrG∘=ΔrH∘−T.ΔrS∘ से कर सकते है तथा अभिक्रिया के लिए तापमान के साथ ΔrH∘ तथा ΔrS∘ के मान में परिवर्तन को निम्न प्रकार परिकलित किया जा सकता है
ΔrH∘T2−ΔrH∘T1=ΔrC∘p(T2−T1)
ΔrS∘T1−ΔrS∘T1=ΔrC∘pln(T2T1)
ΔrG∘=ΔrH∘−TΔrS∘
ΔrG∘=−RTlnKeq द्वारा
निम्न अभिक्रिया पर विचार करें
CO(g)+2H2(g)⇔CH3OH(g)
दिया है :ΔfH∘(CO,g)=−114kJ/mole
S∘(CH3OH,g)=240J/K mol,C∘p,m(H2,g)=29JK−1mol−1
S∘(CO,g)=198J/mol−K,C∘p,m(H2)=28.8 J/mole - K
C∘p,m(CO)=29.4J/mol - K , C∘p,m(CH3OH)=44J/mol-K
तथा ln(320300)=0.06 , सभी आँकड़े 300K पर है।
300K ताप पर अभिक्रिया के लिए ΔrS∘ है
View Solutionअमोनिया का निर्माण अभिक्रिया द्वारा दर्शाया गया है,
N2(g)+3H2(g)→2NH3(g),ΔrH∘=−91.8kJ mol−1
अभिक्रिया के अनुसार, NH3 के विघटन के लिए अभिक्रिया की एन्थैल्पी क्या होगी?
2NH3(g)→N2(g)+3H2(g),ΔrH∘ = ?
View Solutionऊष्मागतिक समीकरण (i), (ii) एवं (iii) के आधार पर, बताइए (a) से (d) तक दिये गये विकल्पों में कौन-सा बीजगणितीय सम्बन्ध सही है?
(i)C(graphite)+O2(g)→CO2(g),ΔrH=xkJ mol−1
(ii)C(graphite)+12O2(g)→CO(g),ΔrH=ykJ mol−1
(iii) CO(g)+12O2(g)→CO2(g),ΔrH=zkJ mol−1
View SolutionLet Δr=∣∣ ∣ ∣∣r−1n6(r−1)22n24n−2(r−1)33n33n2−3n∣∣ ∣ ∣∣. Show that n∑r=1Δr is contant.
View Solutionकिन परिस्थितियों में ECell=0 अथवा ΔrG=0 होगा?
View SolutionFor a chemical reaction A+ B ⇔C+D(ΔrH0=80 KJ mol−1) the entropy change ΔrS0 depends on the temperature T (in K) as (ΔrS0=2T(JK−1mol−1) .
Minimum temperature at which it will become spontaneous is ___________ K. (Integer)
View Solution
