m द्रव्यमान के किसी गोलक को L लंबाई की एक हल्की डोरी से लटकाया जाता है। निम्नतम बिंदु पर इसे 1 वेग प्रदान किया जाता है। यह ऊर्ध्वाधर तल में एक अर्द्धवृत्तीय मार्ग में इस प्रकार व्यवस्थित होती है कि यह केवल तभी ढीली पड़ती है जब गोलक शीर्ष बिंदु C पर पहुँचता है।
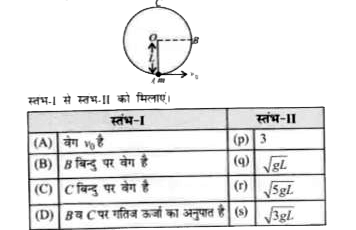
(A)→(p),(B)→(q),(C)→(s),(D)→(r)
(A)→(q),(B)→(r),(C)→(p),(D)→(s)
(A)→(r),(B)→(s),(C)→(q),(D)→(p)
(A)→(s),(B)→(p),(C)→(r),(D)→(q)
The correct Answer is:C
गोलक पर दो बाह्य बल है , डोरी में गुरुत्व (mg ) तथा तनाव (T )l चूँकि विस्थापन हमेशा डोरी के लंबवत होती है तनाव कोई कार्य नहीं करता है।
निस्के की कुल यांत्रिक ऊर्जा (E ) संरक्षित है।
यदि हम न्यूनतम बिंदु A पर किसी निकाय की स्थितिज ऊर्जा शून्य लेते है, तो
A पर , E=12mv20 ...(i)
न्यूटन के द्वितीय नियम से
TA−mg=mv20L ...(ii)
जहाँ A पर डोरी में tanav TA है।
उच्चतम बिंदु C पर,
डोरी (TC) में तनाव शून्य होने के कारण डोरी ढीली पड़ती है। Cपर , E=12mv2c+mg(2L) ...(iii)
न्यूटन के द्वितीय नियम से,
mg=mv2cL ...(iv)
जहाँ C पर वेग vc है।
(iv) से ,vc=√gL
(C)→(q)
(iii) से ,E=12m(gL)+2mgL=52mgl ...(v)
(i ) के प्रयोग से, 12mv20=52mgL
v0=√5gL ...(vi)
(A)→(r)
B प, E=12mv2LB
जहाँ VBB पर वेग है।
या 12mv2B=E−mg(L)=52mgL−mgL((v)के प्रयोग से)
12mv2B=32mgL
∴vB=√3gL
(B)→(s)
B v C पर गतिज ऊर्जाओं का अनुपात,
KBKC=12mv2B12mv2C=3gLgL=31
(D)→(p)
Topper's Solved these Questions
- कार्य, ऊर्जा और शक्ति BOOK - NCERT FINGERTIPS HINDICHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - बहुविकल्प प्रश्न पिटारा (किसी स्प्रिंग की स्थितिज ऊर्जा)
8 Videos
- कार्य, ऊर्जा और शक्ति BOOK - NCERT FINGERTIPS HINDICHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - बहुविकल्प प्रश्न पिटारा (ऊर्जा के विभिन्न रूप : ऊर्जा के संरक्षण का नियम)
4 Videos
- कार्य, ऊर्जा और शक्ति BOOK - NCERT FINGERTIPS HINDICHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - बहुविकल्प प्रश्न पिटारा (स्थितिज ऊर्जा की संकल्पना)
8 Videos
- कणों के निकाय घूर्णी गतिBOOK - NCERT FINGERTIPS HINDICHAPTER - कणों के निकाय घूर्णी गतिEXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
- गति के नियम BOOK - NCERT FINGERTIPS HINDICHAPTER - गति के नियम EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
Similar Questions
एक व्यक्ति किसी बक्से को 1 मीटर की ऊँचाई तक उठाने में 1 मिनट लेता है तथा अन्य व्यक्ति ऐसा ही करने पर 12 मिनट लेता है। दोनों की ऊर्जा है
View Solution1 किग्रा कोल को जलने में ऊर्जा की कितनी मात्रा मुक्त होगी?
View Solutionx दूरी तक खींची गई किसी स्प्रिंग की स्थितिज ऊर्जा 10J है। समान स्प्रिंग को अतिरिक्त दूरी x तक खींचने में किया गया कार्य क्या होगा?
View Solutionनिम्न प्रश्न में, अभिकथन के वक्तव्य के बाद तर्क के वक्तव्य को दिया गया है। सही विकल्प पर निशान लगाइए।
अभिकथनः किसी निकाय के द्रव्यमान केन्द्र की गति का निर्धारण करने के लिए, निकाय के आंतरिक बलों का ज्ञान होना आवश्यक होता है।
तर्कः इस उद्देश्य के लिए हमें निकाय पर बाह्य बलों को जानने की आवश्यकता नहीं होती है।
View Solutionअभिकथन: किसी वस्तु की गति को बनाए रखने के लिए एक बाहरी बल की आवश्यकता होती है।
तर्क: कुल बाह्य बल शून्य है तो विरामावस्था वाली वस्तु विरामावस्था में ही रहेगी तथा गतिमान वस्तु एकसमान वेग से गतिमान रहती है।
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionमंथन के पश्चात दूध को कपड़े के एक टुकड़े पर उढ़ेलने पर क्रीम उस पर रह जाता है। पृथक्करण की यह प्रक्रिया ...... कहलाती है।
View Solutionबच्चों में जन्मजात भाषिक क्षमता होती है। इसका एक शिक्षाशास्त्रीय पक्ष यह है कि पर्याप्त अवसर मिलने पर बच्चा
View Solution30 बच्चो की एक कक्षा में सरन शीर्ष से 9 वे रैंक पर है| मनीष सरन से पांच रैंक निचे है| तल से मनीष की रैंक क्या है?
View Solutionएक बंद पात्र में 25^(@)C पर साम्यावस्था SO_(2)CI_(2)(g) को प्राप्त किया जाता है और एक अक्रिय गैस, हीलियम को प्रवेशित किया जाता है । निम्नलिखित में से कौन सा कथन सही है ?
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionकॉपर पाइराइट अयस्क को वात्या भट्टी में गर्म करके कॉपर को निष्कर्षित किया जाता है, यह विधि इस सिद्धांत पर आधारित है कि
View Solutionएक यौगिक A का अणु सूत्र C_(2)Cl_(3)OH है। यह फेहलिंग विलयन को अपचयित करता है और ऑक्सीकरण पर एक मोनोकार्बोक्सिलिक अम्ल (B) देता है। एथिल ऐल्कोहॉल पर क्लोरीन की क्रिया द्वारा A प्राप्त किया जाता है। A है:
View Solutionजब एसीटैल्डिहाइड को फेहलिंग विलयन के साथ उपचारित किया जाता है, तो यह निम्नलिखित में से किसका अवक्षेप देता है?
View Solutionजब प्रोटीन में पेप्टाइड लिंक टूट जाता है तो निम्न में से किस प्रकार की अभिक्रिया होती है?
View Solution
