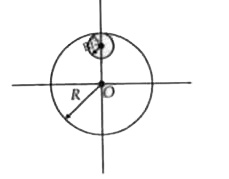
किसी R त्रिज्या तथा 9 M द्रव्यमान की एक वृत्ताकार चकती से, चित्रानुसार, R/3 त्रिज्या वाली एक छोटी सी चकती को हटाया जाता है। तब शेष चकती का इसके तल के लम्बवत् तथा O से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण होता है
4MR2
409MR2
40MR2
379MR2
The correct Answer is:A
चकती का द्रव्यमान प्रति इकाई क्षेत्रफल =9MπR2
चकती के हटाए गए भाग का द्रव्यमान =9MπR2×π(R3)2=M
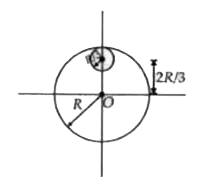
चकती के समतल से लम्बवत् एवं चकती के केन्द्र से गुजरने वाली अक्ष के परितः हटाए गए भाग का जड़त्व आघूर्ण, समान्तर अक्ष प्रमेय का प्रयोग करके, है-
I1=M2(R3)2+M(2R3)2=12MR2
जब चकती के भाग को हटाया नहीं जाए, तो दी गई अक्ष के परित, पूर्ण चकती का जड़त्व आघूर्ण होता है-
I2=92MR2
इसलिए हटाए गए भाग से चकती का जड़त्व-आघूर्ण, दी गई अक्ष के परितः होता है-
I=I2−I1=92MR2−12MR2=4MR2
Topper's Solved these Questions
- कणों के निकाय घूर्णी गतिBOOK - NCERT FINGERTIPS HINDICHAPTER - कणों के निकाय घूर्णी गतिEXERCISE - एन. सी. ई. आर. टी. प्रश्न प्रदर्शिका
8 Videos
- कणों के निकाय घूर्णी गतिBOOK - NCERT FINGERTIPS HINDICHAPTER - कणों के निकाय घूर्णी गतिEXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
- ऊष्मागतिकीBOOK - NCERT FINGERTIPS HINDICHAPTER - ऊष्मागतिकीEXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
- कार्य, ऊर्जा और शक्ति BOOK - NCERT FINGERTIPS HINDICHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
Similar Questions
निम्न में से किसके लिए द्रव्यमान केन्द्र पिण्ड के बाहर स्थित होता है?
View Solutionनिम्न प्रश्न में, अभिकथन के वक्तव्य के बाद तर्क के वक्तव्य को दिया गया है। सही विकल्प पर निशान लगाइए।
अभिकथनः किसी निकाय के द्रव्यमान केन्द्र की गति का निर्धारण करने के लिए, निकाय के आंतरिक बलों का ज्ञान होना आवश्यक होता है।
तर्कः इस उद्देश्य के लिए हमें निकाय पर बाह्य बलों को जानने की आवश्यकता नहीं होती है।
View Solutionप्रक्कथन : रुद्धोष्म प्रक्रम में, किसी गैस की आन्तरिक ऊर्जा में परिवर्तन गैस पर (या द्वारा) किये गये कार्य के तुल्य होती है।
कारण :रुद्धोष्म प्रक्रम में गैस का ताप नियत रहता है।
View Solutionअभिकथनः दो पिण्डों के लिए, न्यूटन के तीसरे नियम से उनके मध्य उत्पन्न पारस्परिक बलों का योग शून्य होता है।
तर्कः दो बलों के द्वारा किए गए कार्य के योग को हमेशा निरस्त करना चाहिए।
View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?
View Solutionहाइड्रोजनपरमाणुकेप्रथमबोरकक्षककीत्रिज्याrहै,तबLi^(2+) के प्रथम कक्षक की त्रिज्या होगी :
View Solutionएक वायु सेना का जहाज 100 किमी/घण्टा की दर से ऊर्ध्वाधरतः ऊपर की और चढ़ रहा है। यदि पृथ्वी की त्रिज्या r किमी है , तब इसके उड़ना शुरू के मिनट बाद जहाज से दिखाई देने वाले पृथ्वी का क्षेत्रफल A=2πr2hr+h जहाँ , h जहाज की पृथ्वी से दूरी है )
View Solutionत्रिज्या r तथा ऊँचाई h वाले बेलन के लिए त्रिज्या के सापेक्ष पृष्ठीय क्षेत्रफल में परिवर्तन की दर ज्ञात करो।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solution8.8cm लम्बा एक रेखाखण्ड AB खींचिए। A को केंद्र मानकर 4 त्रिज्या का एक वृत्त तथा 3 को केंद्र लेकर त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रतेखाओ कि रचना कीजिए।
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionवह समतल, जो बिन्दुओ (−3,−3,4) तथा (3,7,6) को मिलाने वाले रेखाखण्ड का लंबसमद्विभाजक करता है, निम्न में से किस एक बिंदु से होकर जाता है?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionबिंदु hati + 2hatj- hatk से गुजरने वाले तथा hati + 2hatj + hatk से निरूपित बल का बिंदु 2hati + 3hatj + hatk के परितः सदिश आघूर्ण ज्ञात कीजिए|
View Solution
