x−y तल में R त्रिज्या की वृत्तीय कक्षा में एक Q बिन्दु आवेश ω कोणीय गति से परिक्रमा कर रहा है इसे लूप में बहती Qω2π अपरिवर्ती धारा के तुल्य माना जा सकता है अब एकसमान चुंबकीय क्षेत्र को धनात्मक z-दिशा में चालू करते है जिसका मान 0 से B तक एक सैकिण्ड में एकसमान दर से बढ़ता है यह मानिये कि इस दौरान कक्ष की त्रिज्या स्थिर रहती है चुंबकीय क्षेत्र के लगाने से कक्ष में एक emf प्रेरित होता है एक प्रेरित विधुत क्षेत्र द्वारा इकाई धन आवेश को संकृत लूप के चारो ओर घुमाने में किए गये कार्य की मात्रा को प्रेरित विद्युतवाहक बल (emf) कहा जाता है यह ज्ञान है कि जब एक आवेश एक कक्ष में परिभ्रमण करता है तब उसका चुंबकीय द्विध्रुव आघूर्ण उसके कोणीय संवेग के आनुपातिक होता है जिसका अनुपातिक स्थिरांक γ है
जिस समय अन्तराल में चुंबकीय क्षेत्र में परिवर्तन हो रहा है उस अन्तराल के अन्त में आवेश के कक्ष से चुंबकीय द्विध्रुव आघूर्ण में परिवर्तन है
−γBQR2
−γBQR22
γBQR22
γBQR2
The correct Answer is:B
चुम्बकीय द्विध्रुव आघूर्ण M=γJ
ΔM=γΔJ
ΔJΔt=−QdBdt.R2R
Δ=−QB2R2
अतः ΔM=−γQBR22
Topper's Solved these Questions
- विधुत चुम्बकीय प्रेरण BOOK - ERRORLESS HINDICHAPTER - विधुत चुम्बकीय प्रेरण EXERCISE - JEE SECTION (Integer type questions)
2 Videos
- विधुत चुम्बकीय प्रेरण BOOK - ERRORLESS HINDICHAPTER - विधुत चुम्बकीय प्रेरण EXERCISE - JEE SECTION (Matrix Match type questions)
2 Videos
- विधुत चुम्बकीय प्रेरण BOOK - ERRORLESS HINDICHAPTER - विधुत चुम्बकीय प्रेरण EXERCISE - JEE SECTION (Reasoning type questions)
1 Videos
- विद्युत चुम्ब्कीय तरंगे एवं संचारBOOK - ERRORLESS HINDICHAPTER - विद्युत चुम्ब्कीय तरंगे एवं संचारEXERCISE - SELF EVALUATION TEST
12 Videos
- सरल आवर्त गति BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - Self Evaluation Test (सरल आवर्त गति )
19 Videos
Similar Questions
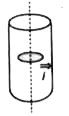
10 मी लम्बी गोल ट्यूब, जिसकी त्रिज्या 0.3 मी है, के वक्रीय-पृष्ठ में। धारा प्रवाहित है (चित्र देखिये)। एक तारलूप, जिसका प्रतिरोध 0.005 ओम तथा त्रिज्या 0.1 मी, ट्यूब के अन्दर रखा है। दोनों के अक्ष एक साथ हैं। धारा i=i0cos (300 t) जहाँ i0 स्थिरांक है। यदि लूप का चुम्बकीय आघूर्ण N μ0i0 sin (300 t), हो, तब N का मान होगा
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View Solutionकथन :ϕB=∮→B.d→S=0 जहाँ ϕB चुम्बकीय फ्लक्स है
कथन-2 : पृथक चुम्बकीय ध्रुव भौतिक विश्व में विधमान नहीं हो सकते है
View Solutionदृष्टि रेडियो संचार की एक पंक्ति में, संचारण और प्राप्त करने वाले एंटेना के बीच लगभग 50 किमी की दूरी रखी जाती है। यदि प्राप्त करने वाले एंटीना की ऊंचाई 70 मीटर है, तो संचारण एंटीना की न्यूनतम ऊंचाई होनी चाहिए: (पृथ्वी की त्रिज्या = 6.4×10^ 6 m)
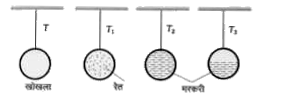
View Solutionएक सरल लोलक , का गोलक एक धात्विक खोकला गोला है। इसका आवर्तकाल T है। जब गोलक में रेत भरी है। तब आवर्तकाल T1 है जब यह मरकरी से भरा है तब आवर्तकाल T2 है जब यह मरकरी से आधा भरा है तब इसका आवर्तकाल T3 है । तब निम्न में से सही विकल्प है।
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionयह ज्ञात है की महाविद्यालय के छात्रों में से 60 % छात्रावास में रहते है और 40 % छात्रावास में नहीं रहते है । पूर्ववर्ती वर्ष से परिणाम सूचित करते है की छात्रावास में रहने वाले छात्रों में से30 % छात्रों में से 20 % छात्रों ने A ग्रेड लिए। वर्ष के अंत में महाविद्यालय के एक छात्र को यादृच्छया चुना गया और पाया गया की उसे A ग्रेड मिला है । इस बात की क्या प्रायिकता है की वह छात्रावास में रहने वाला है ?
View Solutionएक वस्तु जिसका द्रव्यमान m है विराम से h ऊँचाई से गुरुत्वीय त्वरण g के अन्तर्गत गिरती है तथा यह रेत में गहराई d तक धंसती है। रेत में फँसने के दौरान औसत मन्दन होगा
View Solutionएकसमान चुम्बकीय क्षेत्र में आवेश की गति
View Solution30 बच्चो की एक कक्षा में सरन शीर्ष से 9 वे रैंक पर है| मनीष सरन से पांच रैंक निचे है| तल से मनीष की रैंक क्या है?
View Solutionएक ठोस AB की NaCl प्रकार की संरचना है जिसकी कोर लम्बाई 580. 4 pm है। A+ की त्रिज्या 100 pm है। pm में B− की त्रिज्या क्या है?
View Solutionनिम्नलिखित में से किसे एक कैंसररोधी प्रजाति माना जाता है?
View Solution""_ZX^A के रेडियोधर्मी क्षय में, निम्नलिखित में से किसे अशुद्ध कथन के रूप में माना जा सकता है?
View Solutionनिम्नलिखित में से किस आयन की आयनिक त्रिज्या का उच्चतम मान है?
View Solutionएक अभिक्रिया की सक्रियण ऊर्जा को निम्न में से किस ग्राफ की प्रवणता से निर्धारित किया जा सकता है?
View Solutionनिम्नलिखित में से कौन एक लूइस अम्ल की तरह व्यवहार नहीं कर सकता है?
View Solution
