एक लम्बी परिनालिका S में व्यास a के साथ प्रति मीटर n फेरे हैं। इस कुंडली के केन्द्र में, हम N फेरे एवं व्यास b(b < a) की एक छोटी कुंडली को रखते हैं। यदि परिनालिका में धारा समय के साथ रेखीय रूप से बढ़ती है, तो वि. वा. बल छोटी कुंडली में प्रेरित होगा। यदि धारा mt2+C के फलन के रूप में परिवर्तित होती है तो निम्न में से कौन-सा |ε| नाम t दर्शाने वाला ग्राफ सही है?

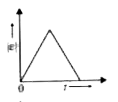


The correct Answer is:C
प्रश्न में दिये गये डाटा के अनुसार, परिनालिका S में धारा के कारण चुम्बकीय क्षेत्र, B=μ0nI
इस क्षेत्र के कारण सबसे छोटी कुंडली से जुड़ा चुम्बकीय फ्लक्स,
ϕ=NBA, जहाँ A = छोटी कुंडली का क्षेत्रफल =πb2
∴ छोटी कुंडली में प्रेरित वि.वा.बल.
ε=−dϕdt=−ddt(NBπb2)
=−Nπb2dIdt(μ0n)=−Nπb2μ0ndIdt
चूँकि धारा I, (mt2+C) के फलन की भाँति परिवर्तित होती है,
∴ε=−Nnμ0nb2ddt(mt2+C)
=−Nnπμ0b2(2mt) ...(i)
(1) से, |ε|∝t
इसलिए सही विकल्प (c) है।
Topper's Solved these Questions
- विद्युतचुम्बकीय प्रेरणBOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युतचुम्बकीय प्रेरणEXERCISE - बहुविकल्प प्रश्न पिटारा (लेंज का नियम एवं ऊर्जा का संरक्षण)
13 Videos
- विद्युतचुम्बकीय प्रेरणBOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युतचुम्बकीय प्रेरणEXERCISE - बहुविकल्प प्रश्न पिटारा (गतिक विद्युतवाहक बल )
16 Videos
- विद्युतचुम्बकीय प्रेरणBOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युतचुम्बकीय प्रेरणEXERCISE - बहुविकल्प प्रश्न पिटारा (चुम्बकीय फ्लक्स)
6 Videos
- विद्युत धारा BOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युत धारा EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
- विधुतचुम्बकीय तरंगे BOOK - NCERT FINGERTIPS HINDICHAPTER - विधुतचुम्बकीय तरंगे EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
Similar Questions
किसी चुम्बकीय क्षेत्र में गतिमान तार में प्रेरित धारा की दिशा किसका प्रयोग करके प्राप्त की जाती है?
View Solutionएक वृत्तीय कुंडली चुम्बकीय क्षेत्र के क्षेत्र में अरीय (Radially) रूप से प्रसारित होती है तथा कुंडली में कोई विद्युत वाहक बल उत्पन्न नहीं होता है। ऐसा होता है क्योंकि
View Solutionक्षेत्र B के समानान्तर इसके तल के साथ रखे गये अनुप्रस्थ परिच्छेद क्षेत्रफल A के N फेरों की कुंडली के साथ जुड़ा चुम्बकीय फ्लक्स होता है-
View Solutionअभिकथन: विद्युत वाहक बल एक ऐसा बल होता है जो इलेक्ट्रॉन के प्रवाह एवं धारा उत्पन्न करने में मदद करता है।
तर्कः विद्युत वाहक बल सेल में वोल्टता पर निर्भर नहीं करता है।
View Solutionअभिकथनः विभिन्न प्रकार की विद्युतचुम्बकीय तरंगों के बीच मुख्य अन्तर उनकी तरंगदैर्घ्य या आवृत्तियों में होता है।
तर्क: विद्युतचुम्बकीय तरंगें समान चाल से निर्वात में गति करती हैं।
View Solutionएक कुंडली को जिसका प्रेरण 0.50 तथा प्रतिरोध 100Ω है 240V व 50HZ की एक आपूर्ति से जोड़ा गया हैं | (a)कुंडली में अधिकतम धारा कितनी है? (b) वोल्टेज शीर्ष व् धारा शीर्ष के बीच समय-पश्चता कितनी है ?
यदि परिपथ को उच्च आवृत्ति की आपूर्ति ( 240 V , 10 kHz ) से जोड़ा जाता है तो अभ्यास 7.13 (a) तथा (b) के उत्तर निकालिए इसके इस कथन की व्याख्या कीजिए कि अति उच्च आवृत्ति पर किसी परिपथ में प्रेरक लगभग खुले परिपथ के तुल्य होता है स्थिर अवस्था के पश्चात किसी dc परिपथ में प्रेरक किस प्रकार का व्यवहार करता है
View Solutionयदि शब्द PROBABILITY के अक्षर एक पंक्ति में यदृच्छया लिखे जाते है तो दो के साथ आने की प्रायिकता है -
View Solutionआइये जाने किसी कुंडली में धारा कैसे प्रेरित होती है
View Solutionयदि सुलेखा रेलगाड़ी' को रेलगाडि' लिखती है तो एक भाषा-शिक्षक के रूप में आप क्या करेंगे?
View SolutionIf PLAIN is coded as NJYGL, then MUG is coded as ____. यदि एक निश्चित कोड भाषा में,'PLAIN' को NJYGL के रूप में लिखा जाता है, तो उस भाषा में MUG कैसे लिखा जाएगा ?
View SolutionIn a certain code language, U is written as A, A as G, D as I, N as T, B as R, E as D and C as U. How will ABUNDANCE be written in that code? एक निश्चित कोड भाषा में,U को A के रूप में, A को G के रूप में, D को I के रूप में, N को T के रूप में, B को R के रूप में, E को D के रूप में, और C के रूप में लिखा जाता है। उस कोड में ABUNDANCE कैसे लिखा जाएगा?
View SolutionIn a certain code language, G is written as S, L as A, A as O, O as N, N as E, E as G, H as L and S as H. How will HALOGENS be written in that code?
एक निश्चित कोड भाषा में,G को S के रूप में लिखा जाता है, L को A के रूप में, A को O के रूप में, O को N के रूप में, N को E के रूप में, E को G के रूप में, H को L के रूप में और S को H के रूप में लिखा जाता है। उस कोड में HALOGENS कैसे लिखेंगे ?
View SolutionIn a certain code language I is written as P, L as A, A as O, O as N, N as C, C as T, P as L and T as I. How will POLITICIAN be written in that code? एक निश्चित कोड भाषा में, I को P के रूप में लिखा जाता है, L को A के रूप में, A को O के रूप में, O को N के रूप में, N को C के रूप में, C को T के रूप में, P को L के रूप में, T को I के रूप में, लिखा जाता है। उसी कोड में POLITICIAN को कैसे लिखेंगे?
View Solutionकॉपर के वैद्युत् परिष्करण के प्रक्रम के समय, अशुद्धि के रूप में उपस्थित कुछ धातुएं ऐनोड पंक के रूप में नीचे बैठ जाती हैं। ये हैं:
View Solutionग्लूकोज के ताजा तैयार विलयन से समय के साथ प्रकाशिक घूर्णन में परिवर्तन को निम्न में जाना जाता है -
View Solutionनिम्नलिखित में से कौनसी अभिक्रिया में हाइड्रोजन परॉक्साइड, एक ऑक्सीकारक के रूप में कार्य करता है?
View Solution
