एक चुंबकीय क्षेत्र B, r a क्षेत्र तक सीमित है तथा पेपर की ओर उन्मुख है (z अक्ष), r=0 वृत्तीय क्षेत्र के केन्द्र से होते हुए। b (b a) त्रिज्या तथा m द्रव्यमान का एक आवेशित वलय (Charge q) मूल पर अपने केन्द्र के साथ x-y तल में स्थित है। वलय (Ring) घूर्णन के लिए स्वतंत्र है तथा विरामावस्था में है। चुम्बकीय क्षेत्र t समय में शून्य पर लाया जाता है। क्षेत्र के समाप्त होने पर वलय का कोणीय वेग होगा-
The correct Answer is:D
माना E, त्रिज्या b की आवेशित वलय के चारों ओर उत्पन्न विद्युत क्षेत्र है, तो
…(i)
वलय पर कार्यरत बल आघूर्ण, = b x बल = bqE
[(i) से]
यदि आवेशित वलय के कोणीय संवेग में परिवर्तन है, तो
चूँकि प्रारंभिक कोणीय संवेग,
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युतचुम्बकीय प्रेरणEXERCISE - बहुविकल्प प्रश्न पिटारा (लेंज का नियम एवं ऊर्जा का संरक्षण)13videos
विद्युतचुम्बकीय प्रेरण
- BOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युतचुम्बकीय प्रेरणEXERCISE - बहुविकल्प प्रश्न पिटारा (गतिक विद्युतवाहक बल )16videos
विद्युतचुम्बकीय प्रेरण
- BOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युतचुम्बकीय प्रेरणEXERCISE - बहुविकल्प प्रश्न पिटारा (चुम्बकीय फ्लक्स)6videos
विद्युतचुम्बकीय प्रेरण
- BOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युत धारा EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न15videos
विद्युत धारा
- BOOK - NCERT FINGERTIPS HINDICHAPTER - विधुतचुम्बकीय तरंगे EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न15videos
विधुतचुम्बकीय तरंगे
Similar Questions
किसी चुम्बकीय क्षेत्र में गतिमान तार में प्रेरित धारा की दिशा किसका प्रयोग करके प्राप्त की जाती है?
06:33View Solutionएक वृत्तीय कुंडली चुम्बकीय क्षेत्र के क्षेत्र में अरीय (Radially) रूप से प्रसारित होती है तथा कुंडली में कोई विद्युत वाहक बल उत्पन्न नहीं होता है। ऐसा होता है क्योंकि
04:26View Solutionक्षेत्र B के समानान्तर इसके तल के साथ रखे गये अनुप्रस्थ परिच्छेद क्षेत्रफल A के N फेरों की कुंडली के साथ जुड़ा चुम्बकीय फ्लक्स होता है-
41:18View Solutionअभिकथन: विद्युत वाहक बल एक ऐसा बल होता है जो इलेक्ट्रॉन के प्रवाह एवं धारा उत्पन्न करने में मदद करता है।
तर्कः विद्युत वाहक बल सेल में वोल्टता पर निर्भर नहीं करता है।53:48View Solutionअभिकथनः विभिन्न प्रकार की विद्युतचुम्बकीय तरंगों के बीच मुख्य अन्तर उनकी तरंगदैर्घ्य या आवृत्तियों में होता है।
तर्क: विद्युतचुम्बकीय तरंगें समान चाल से निर्वात में गति करती हैं।58:30View Solutionचित्र में दिखाए गए छायांकित क्षेत्र के लिए असामिका है-
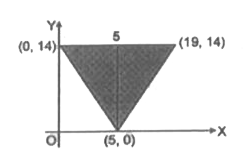 View Solution
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
01:29:51View Solutionचुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता | एक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता
01:24:31View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष तथा केन्द्र पर चुंबकीय क्षेत्र | ऐम्पियर का परिपथीय नियम
38:24View Solutionएक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल | संयुक्त विद्युत चुम्बकीय क्षेत्र में आवेशित कण की गति
36:33View Solutionनिम्नलिखित कॉलम को सुमेलित कीजिये
कॉलम-I कॉलम-II(A) एक समान आवेशित परावैधुत वलय(p) निकाय के बाहर नियत स्थिर विधुत क्षेत्र है(B) एक सामान आवेशित परावैधुत वलय कोणीय वेग ωसे घूर्णित है (q)चुम्बकीय क्षेत्र की तीव्रता(C) वलय में नियत धारा i(r)वैधुत क्षेत्र (प्रेरित)(D)i=i0cosωt(s) चुम्बकीय द्वि - ध्रुव आघूर्ण43:52View Solutionआवेशित वलय के कारण उसकी अक्ष पर विद्युत क्षेत्र
40:13View Solutionसमरूप आवेशित वलय के कारण उसकी अक्ष पर विद्युत क्षेत्र
07:31View Solutionधारावाही वलय , पट्टिका के कारण चुंबकीय क्षेत्र
45:31View Solutionधरावाही वलय के अक्ष पर चुंबकीय क्षेत्र
56:57View Solutionधारावाही वलय के अक्ष पर चुंबकीय क्षेत्र
01:23:57View Solution

