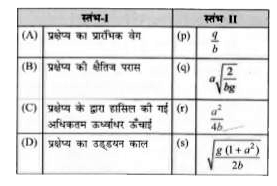
किसी प्रक्षेप्य की गति का समीकरण है, जहाँ a एवं b गति के नियतांक है। स्तंभ-I की राशियों को स्तंभ-II के संबंधो से मिलान कीजिए।
The correct Answer is:C
दिए गए समीकरण, की प्रक्षेप्य गति के समीकरण से तुलना करने पर,
…(i)
तथा …(ii)
या
या ( (i) के प्रयोग से )
या
(A) to (s)
(B) क्षैतिज परास
( (i) व का प्रयोग करके )
(B) to (p)
(C ) अधिकतम ऊँचाई
( (i) व (ii) के प्रयोग से )
(C ) to (r)
(D) (ii) से,
या या ...(iii)
उड्डयन काल
( (i) व (ii) के प्रयोग से )
(D) to (q)
Topper's Solved these Questions
- समतल में गति BOOK - NCERT FINGERTIPS HINDICHAPTER - समतल में गति EXERCISE - बहुविकल्प प्रश्न पिटारा - एकसमान वृत्तीय गति
14 Videos
- समतल में गति BOOK - NCERT FINGERTIPS HINDICHAPTER - समतल में गति EXERCISE - बहुविकल्प प्रश्न पिटारा - विविध प्रश्न
13 Videos
- समतल में गति BOOK - NCERT FINGERTIPS HINDICHAPTER - समतल में गति EXERCISE - बहुविकल्प प्रश्न पिटारा - द्विविमीय गति में आपेक्षिक वेग
4 Videos
- मात्रक एवं मापन BOOK - NCERT FINGERTIPS HINDICHAPTER - मात्रक एवं मापन EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
- सरल रेखा में गति BOOK - NCERT FINGERTIPS HINDICHAPTER - सरल रेखा में गति EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
Similar Questions
एक साइकिल चालक 1 km की त्रिज्या वाले एक वृत्तीय पार्क के केन्द्र से अपनी यात्रा शुरू करता है तथा OPRQO मार्ग के साथ - साथ चित्रानुसार गति करता है। यदि वह 10 m/s की निरंतर गति को बनाए रखता हो, तब बिन्दु R पर त्वरण क्या होगा ?

View Solutionयदि सदिशों →A व →B के मध्य का कोण θ हैं, तो गुणनफल (→B×→A).→A का मान बराबर हैं -
View Solutionएक नदी पश्चिम से पूर्व की ओर 5 m/s की चाल से बह रही हैं। एक तैराक शान्त जल में 10 m/s की चाल से तैर सकता हैं। यदि वह दक्षिणी किनारे पर बिन्दु A से प्रारम्भ करके नदी के उत्तरी किनारे पर बिन्दु B पर पहुँचना चाहता हैं, तो उसे किस दिशा में तैरना चाहिए। ?
View Solutionअभिकथन : बल को दाब में जोड़ा जा सकता है।
तर्क : बल व दाब की विमाएँ समान होती हैं।
View Solutionअभिकथन किसी वस्तु को एकविमीय चाल में, पथ की लंबाई विस्थापन के बराबर होती है।
तर्क: वस्तु की दिशा दो बार परिवर्तित होती है।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View SolutionExam Special|गति के समीकरण की व्याख्या
View Solutionग्राफ की सहायता से गति के समीकरणों को व्युत्पन्न करना
View Solutionगति के समीकरण गणितीय विधि से #!#गति का द्वितीय समीकरण
View Solutionऊंचाई के टॉवर से क्षैतिज प्रक्षेप्य गति
View SolutionMatch the source in column B with the product of Column A. स्तंभ 'ब' के स्रोत का मिलान स्तंभ 'अ के उत्पाद के साथ करें।
View Solutionस्तंभ I का स्तंभ II के साथ मिलान कीजिए और उचित विकल्प चिह्नित कीजिए।
View Solutionस्तंभ I का स्तंभ II के साथ मिलान कीजिए और उचित विकल्प चिह्नित कीजिए।
View Solutionस्तंभ II में दिए गए आवर्त के साथ स्तंभ I में दिए गए तत्वों के परमाणु क्रमांक का मिलान कीजिए और उपयुक्त चयन को चिह्नित कीजिए।
View Solutionस्तंभ | का स्तंभ || के साथ मिलान कीजिए और उचित विकल्प चिह्नित कीजिए।
View Solutionस्तंभ | का स्तंभ || के साथ मिलान कीजिए और उचित विकल्प को चिह्नित कीजिए।
View Solution
