यदि xn>xn−1>….>x2>x1>1 तो का मान है
0
1
2
इनमे से कोई नहीं
The correct Answer is:B
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - JEE Advanced (More than one correct answers)5videos
लघुगणक और आंशिक भिन्नें
- BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - JEE Advanced (integer type questions)8videos
लघुगणक और आंशिक भिन्नें
- BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - SOLVED MULTIPLE CHOICE QUESTIONS (आंशिक भिन्ने)11videos
लघुगणक और आंशिक भिन्नें
- BOOK - ERRORLESS HINDICHAPTER - फलन, सीमा, सांतत्य तथा अवकलनीयताEXERCISE - JEE ADVANCED( MATCH THE COLUMN TYPE)13videos
फलन, सीमा, सांतत्य तथा अवकलनीयता
- BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - JEE Advanced (Matrix Match type questions)2videos
वर्ग समीकरण एवं असमिकायें
Similar Questions
यदि 3x=4x−1, तब x=
02:17View Solutionपद 6+log32⎛⎜ ⎜⎝13√2 ⎷4−13√2 ⎷4−13√2√4−13√2…⎞⎟ ⎟⎠ का मान है
02:08View Solutionयदि 2x+3(x+1)(x−3)=ax+1+bx−3 तो a+b=
03:54View Solutionकॉलम I में दिए गए वक्तव्यों/व्यंजकों का कॉलम II में दिये गये मानों से सुमेल करे।
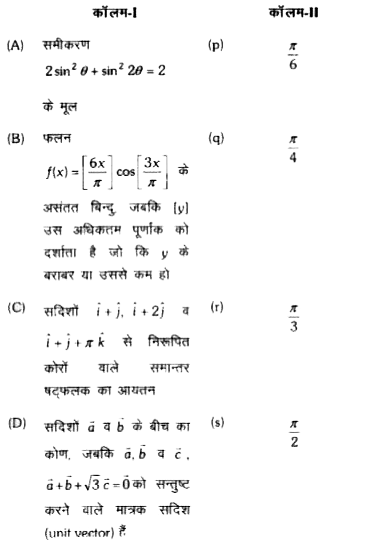
View Solution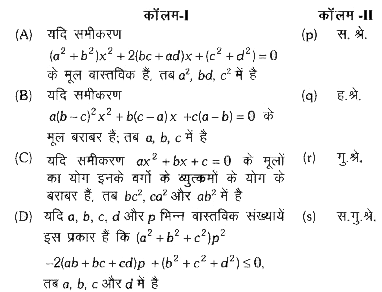
04:37View SolutionIf the arithmetic mean of the observations x1,x2,x3,........,xn is 1, then the arithmetic mean of x1k,x2k,x3k,......,xnk(k>0) is
10:12View SolutionIf f:N→N,andx2>x1⇒f(x2)>f(x)∀x1,x2∈Nandf(f(n))=3n∀n∈N, then f(2)= _______.
02:38View SolutionThe constraints −x1+x2<1,−x1+3x2≤9,x1,x2>,0 difines on
02:18View SolutionLet a sequence x1,x2,x3,… of complex numbers be defined by x1=0,xn+1=x2n−i for all n>1, where i2=−1. Find the distance of x2000 from x1997 in the complex plane.
03:05View SolutionLet x1 and x2(x1>x2) be roots of the equation sin−1(cos(tan−1(cosec(cot−1x))))=π6, then
View Solutionयदि x1x2,x3,......समान्तर श्रेणी में हों तथा xi>0, सभी i के लिए, तो सिध्द कीजिए कि
1√x1+√x2+1√x2+√x3+.....1√xn−1+√xn=n−1√x1+√xn04:04View SolutionLet f'(x)>0andf''(x)<0 where x1<x2.
Then show f(x1+x22)>f(x1)+f(x2)203:15View SolutionIf f:N→N,andx2>x1⇒f(x2)>f(x)∀x1,x2∈Nandf(f(n))=3n∀n∈N, then f(2)= _______.
03:40View SolutionProve the inequality
arc tanx2−arctanx1<x2−x1 where x2>x102:58View SolutionProve that Bernoulli inqeuality (1+x1)[1+x2).....(1+xn)≥1+x1+x2+......+xn. Where x1,x2,.....xn are numbers of like sign, and 1+x1>0(i=1,2,.....n)
05:48View Solution