तनयहीन लम्बाई L तथा नगण्य द्रव्यमान की एक स्प्रिंग जिसके एक सिरे से कम द्रव्यमान m लटकाया गया है , कोणीय आवर्ती ω0 के साथ ऊर्ध्वाधर दोलन कर रही है। जब स्प्रिंग के दूसरे सिरे को स्थाई बिंदु पर रखकर द्रव्यमान को कोणीय गति ω के साथ घुमाया जाता है तब द्रव्यमान क्षैतिज समतल में वृतीय पथ पर एक समान गति करने लगता है। इस घूर्णन के दौरान स्प्रिंग की लम्बाई में वृद्धि होगी।
ω2Lω20−ω2
ω20Lω2−ω20
ω−02Lω20
ω20Lω2
The correct Answer is:A
Kxsinθ=mω2(L+x) और √Km=ω0
K=mω20
mω20x=mω2(L+x)⇒x=ω2Lω20−ω2
Topper's Solved these Questions
- सरल आवर्त गति BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - Ordinary Thinking ( Objective Question) (सरल आवर्त गतियों का अध्यारोपण एवं अनुनाद )
10 Videos
- सरल आवर्त गति BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - Critical Thinking (Objective Question)
51 Videos
- सरल आवर्त गति BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - Ordinary Thinking ( Objective Question) (सरल लोलक )
39 Videos
- विधुत चुम्बकीय प्रेरण BOOK - ERRORLESS HINDICHAPTER - विधुत चुम्बकीय प्रेरण EXERCISE - Self Evaluation Test विधुत चुम्बकीय प्रेरण
17 Videos
- स्थिर वैद्युतBOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Self Evaluation Test
8 Videos
Similar Questions
दो सरल आवर्त गतियां निम्न समीकरण द्वारा प्रदर्शित है
y1=5(sin2πt+√3cos2πt) तथा y2=5sin(2πt+π4)
इन दोनों के आयामों का अनुपात होगा।
View Solutionदो कण समान आयाम तथा समान आवृति के साथ एक सीधी रेखा में स. आ. ग. (S.H.M. ) कर रहे है|अब दोनों कण एक दूसरे को पार करके विपरीत दिशा में जाते है तब उनका विस्थापन आयाम का आधा होता है। इन कणों के बीच कलांतर होगा।
View Solutionसरल लोलक का आवृतकाल दुगुना हो जाएगा जबकि
View Solutionचित्र में चार तार लूपो को दिखाया गया है। जिनकी भुजाओ की लम्बाई L या 2L है सभी चारो एकसमान वेग से एक समरूप चुम्बकीय क्षेत्र →B (कागज़ तल के लम्बवत बाहर की ओर) से गुजरते है। जब ये चुम्बकीय क्षेत्र से गुजरते है तब इनमे उत्पन्न वि. वा. बल. के परिमाण के आधार पर इसका क्रम क्या होगा
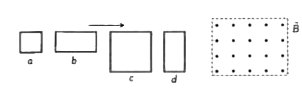
View Solutionनिम्न चार स्थितियों में आवेशित कण मूल बिंदु से बराबर - बराबर दूरियों पर स्थित हैं मूल बिंदु क्षेत्र के परिमाण को अधिकतम पहले लेते हुये इन्हें व्यवस्थित करें
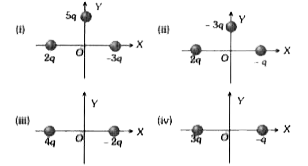
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solution10 g द्रव्यमान और 50 m/s चाल वाली बंदूक की गोली एक दरवाजे में अंतः स्थापित हो जाती है । दरवाजा 1.0 M चौड़ा है और इसका द्रव्यमान 12 kg है इसके एक सिरे पर कब्जे लगे है और यह इनसे गुजरती एक ऊर्ध्वाधर अक्ष के परितः लगभग बिना घर्षण के घूम सकता है । गोली के दरवाजे में अंतः स्थापन के ठीक बाद इसका कोणीय वेग ज्ञात कीजिए ।
View SolutionL लम्बाई की एक छड़ जिसके सिरे दो परस्पर लम्ब रेखाओं पर स्थित है , फिसलती है । छड़ को 1:2 के अनुपात में विभाजित करने वाले बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक कण y=x2+2x से साथ-साथ चलता है। व्रक के किस बिंदु पर x तथा y निर्देशांक समान दर से परिवर्तित हो रहे है ?
View Solutionएक 5 kg द्रव्यमान वाली वस्तु पर 2s के लिये एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3m/s से बढा 7m/s कर देता है। लगाये गये बल की मात्रा ज्ञात करें
View Solutionजब एक धातु को सिल्वर (Ag) के साथ विद्युत्-लेपित किया जाता है, तब
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionआण्विक द्रव्यमान 390 वाले एक यौगिक को प्राप्त करने के लिए आण्विक द्रव्यमान 180 वाले एक यौगिक को CH_(3)COCl के साथ ऐसिलीकृत किया जाता है। पूर्व यौगिक के प्रति अणु पर उपस्थित ऐमीनो समूहों की संख्या है:
View Solutionसमान परिस्थितियों में H2,O2 और मेथेन के समान द्रव्यमान को 27∘C पर आयतन V के एक पात्र में लिया गया है। H2:O2 : मेथेन गैसों के आयतन का अनुपात होगा:
View Solutionएक साइक्लोहेक्सेनोन, अम्ल उत्प्रेरक मात्रा की उपस्थिति में डाइमेथिलएमीन के साथ अभिक्रिया पर एक यौगिक का निर्माण करता है, यदि अभिक्रिया के दौरान जल का लगातार निष्कासन किया जाता है, तब निर्मित यौगिक को सामान्यतः जाना जाता है
View Solutionसल्फर के एक यौगिक में द्रव्यमान द्वारा 8% सल्फर उपस्थित होता है। यौगिक के न्यूनतम आण्विक द्रव्यमान की गणना कीजिए।
View Solution
