यदि secθ=m और tanθ=n, तब 1m[(m+n)+1(m+n)] =
2
2m
2n
mn
The correct Answer is:A
Step by step video, text & image solution for यदि sectheta=m और tantheta=n, तब (1)/(m)[(m+n)+(1)/((m+n))] = by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - Multiple Choice Questions (दो एवं तीन कोणों के योग व अन्तर के त्रिकोणमितीय अनुपात )
48 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - Multiple Choice Questions (अपवर्त्य और उप -अपवर्त्य कोणों के त्रिकोणमितीय अनुपात )
23 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)
5 Videos
- त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - JEE Advanced
47 Videos
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (Matrix Match type questions)
4 Videos
Similar Questions
यदि sinA+sinB=C तथा cosA+cosB=D, तो sin(A+B)=
View Solutionयदि cos2B=cos(A+C)cos(A−C) तो tanA,tanB,tanC है
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
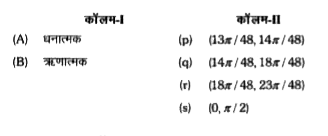
View Solution0<θ<π2 के लिए 6Σm=1cosec(θ+(m−1)π4)cosec(θ+mπ4)=4√2 का के हल निम्न है।
View Solutionमाना निम्न रैखिक समीकरण है ax+by+cz=0,bx+cy+oz=0,cx+ay+bz=0 कॉलम । में दी गयी स्थितियों/व्यंजकों का कॉलम ॥ में दिए गए वक्तव्यों से सुमेल करें

View Solution2{(m-n)/(m+n)+1/3((m-n)/(m+n))^(3)+1/5((m-n)/(m+n))^(5) +..} is equals to
View Solutionm.(tanθ−30)=n(tanθ+120) then,m+nm−n=
View SolutionIf sec theta = m " और " tan theta = n " तब" 1/m [(m + n) + 1/((m+n))] Find the value of
View SolutionIf sintheta+costheta=m And sectheta+cosectheta=n , so n(m+1)(m-1) =
View SolutionProve that 1(m!)nC0+n((m+1)!)nC1+n(n−1)((m+2)!)nC2++n(n−1)2×1((m+n)!)nCn=(m+n+1)(m+n+2)(m+2n)(m+n)!
View SolutionIfIm,n=∫π20sinmxcosnxdx, Then show that Im,n=m−1m+nIm−2,n(m,n∈N) Hence, prove that Im,n=f(x)={(n−1)(n−3)(m−5)(n−1)(n−3)(n−5)(m+n)(m+n−2)(m+n−4)π4 when both m and n are even
(m−1)(m−3)(m−5)(n−1)(n−3)(n−5)(m+n)(m+n−2)(m+n−4)}
View SolutionIf tanθ+sinθ=m and tanθ−sinθ=n, show that m2−n2=4√nm
View SolutionTan−1(mn)−Tan−1(m−nm+n)=
View SolutionIf secθ=m,tanθ=n, then 1m[(m+n)+1m+n]....................... A) 2 B) 2m C) 2n D) mn
View SolutionIf I(m,n)=∫10tm(1+t)n.dt, then the expression
for I(m,n) in terms of I(m+1,n-1) is:
(a) 2nm+1−nm+1I(m+1,n−1)
(b) nm+1I(m+1,n−1)
(c) 2nm+1+nm+1I(m+1,n−1)
(d) mm+1I(m+1,n−1)
View Solution
