फलन f(a)=logex, मध्यमान प्रमेय की शर्तों को [1,3] में संतुष्ट करता है , तो c का मान है
2log3e
12loge3
log3e
loge3
The correct Answer is:A
Step by step video, text & image solution for फलन f(a)=log_(e)x, मध्यमान प्रमेय की शर्तों को [1,3] में संतुष्ट करता है , तो c का मान है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- अवकलन तथा अवकलज के अनुप्रयोगBOOK - ERRORLESS HINDICHAPTER - अवकलन तथा अवकलज के अनुप्रयोगEXERCISE - MULTIPLE CHOICE QUESTIONS (एक बिन्दु पर अवकलज,मानक अवकलज)
186 Videos
- अवकलन तथा अवकलज के अनुप्रयोगBOOK - ERRORLESS HINDICHAPTER - अवकलन तथा अवकलज के अनुप्रयोगEXERCISE - MULTIPLE CHOICE QUESTIONS (अस्पष्ट फलनों का अवकलन,प्रचलिक व संयुक्त फलनों का अवकलन,लघुगणकीय अवकलन, अनन्त श्रेणियों के अवकलन )
64 Videos
- अवकल समीकरण BOOK - ERRORLESS HINDICHAPTER - अवकल समीकरण EXERCISE - JEE Advanced ( Matrix Match type questions )
3 Videos
- केन्द्रीय प्रवृत्ति के मापBOOK - ERRORLESS HINDICHAPTER - केन्द्रीय प्रवृत्ति के मापEXERCISE - Jee Advanced (Reasoning )
2 Videos
Similar Questions
2f(x)=f'(x) एवं f(0)=3, तब f(2)=
View Solutionमाना y,x2x−2xxcoty−1=0 से परिभाषित x का एक अस्पष्ट फलन है। तब y'(1) बराबर है
View Solution
View Solutionकथन - 1 : प्रथम n सम धन पूर्णांकों का प्रसरण n2−14 है।
कथन - 2 : प्रथम n धन पूर्णाको का योगफल n(n+1)2 और प्रथम n धन पूर्णांको के वर्गों का योगफल n(n+1)(2n+1)6 है।
View Solutionफलन f(x)=2sinx का आयाम है -
View Solutionयदि फलन f(x) द्वारा अधिकतम मान x व y न्यूनतम मान ग्रहण किया जाता है तो इस फलन का आयाम . . . . . . . है ।
View Solutionआकृति में O वृत्त का केंद्र है। यदि ∠APB=70∘ तो ∠AQB का मान है -
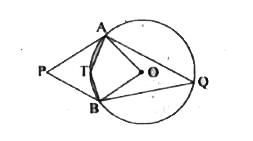
View Solutiona का न्यूनतम मान ज्ञात कीजिए कि फलन f(x)=x2+ax+5 अंतराल [1, 2] में वर्धमान है।
View Solutionलाग्राज मध्यमान प्रमेय f(a+h)−f(a)=hf'(a+θh) में जहाँ θ∈(0,1) फलन f(x)=x2 के लिए θ का मान ज्ञात कीजिए।
View Solutionयदि फलन f(x)=(x−3)(x−4)∀x∈[0,4] है तो लाग्राज मध्यमान प्रमेय सत्यापित कर c का मान ज्ञात करो।
View Solutionफलन के लिए लाग्राज मध्यमान प्रमेय की सत्यता की जांच कीजिए
f(x)=x2−4x−1,x∈[0,2]
View Solutionफलन के लिए लाग्राज मध्यमान प्रमेय की सत्यता की जांच कीजिए
f(x)=⎧⎪⎨⎪⎩1+xx≤2यदि5−xx≥2,x∈[1,3]
View Solutionफलन के लिए लाग्राज मध्यमान प्रमेय की सत्यता की जांच कीजिए
f(x)={(1+x,,,x<2,),(,,,),(5−x,,,x≥2,),x∈[1,3]
View Solutionयदि फलन f (x) आवर्त का सतत फलन है , तो समाकलन I=∫a+Taf(x)dx का मान है
View Solutionएक फलन g जो प्रत्येक वास्तविक संख्या x>0 के लिए परिभाषित है तथा g(1)=1,g'(x2)=x3 को सभी x>0 के लिए सन्तुष्ट करता है, तो g (4) का मान है
View Solutionयदि सरल रेखा y = 2x + c, परवलय y2=4x को स्पर्श करता है, तो c का मान है |
View Solution
