व्यंजक (cos223∘–sin267∘) का मान धनात्मक है।
Step by step video & image solution for व्यंजक (cos^2 23^(@) – sin^2 67^(@)) का मान धनात्मक है। by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमिति का परिचय और उसके अनुप्रयोग BOOK - NCERT EXEMPLAR HINDICHAPTER - त्रिकोणमिति का परिचय और उसके अनुप्रयोग EXERCISE - प्रश्नावली 8.3
15 Videos
- त्रिकोणमिति का परिचय और उसके अनुप्रयोग BOOK - NCERT EXEMPLAR HINDICHAPTER - त्रिकोणमिति का परिचय और उसके अनुप्रयोग EXERCISE - प्रश्नावली 8.4
18 Videos
- त्रिकोणमिति का परिचय और उसके अनुप्रयोग BOOK - NCERT EXEMPLAR HINDICHAPTER - त्रिकोणमिति का परिचय और उसके अनुप्रयोग EXERCISE - प्रश्नावली 8.1
15 Videos
- त्रिभुज BOOK - NCERT EXEMPLAR HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6.4
18 Videos
Similar Questions
sinθ1+cosθ+1+cosθsinθ=2cosecθ
View Solutionयदि cosecθ+cotθ=p है, तो सिद्ध कीजिए कि cosθ=p2−1p2+1 है
View Solutionयदि cosA=45 है, तो tanA का मान है
View Solutionआकृति 6.16 में, यदि ∠A=∠C,AB=6cm,AP=12cm,BP=15cm, और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।
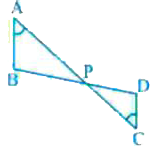
View SolutionWhat is the value of (cos267∘−sin223∘)?
View Solution2cosec223∘ cos267∘−sin223−2cosec223∘cot267∘−sin223∘−sin267−cot267∘ किसके बराबर है?
View SolutionThe value of the expression (cos223∘−sin267∘) is
View Solutionसिद्ध करें कि
sin267∘+sin223∘=cos289∘+cos21∘=1
View Solutionव्यंजक ∣∣¯aׯb∣∣2+(¯a.¯b)2 का मान ........ है |
View Solutionλ का वह धनात्मक मान जिसके लिए व्यंजक x2(√x+λx2)10 में x2 का गुणांक 720 है, है
View Solution2cosec223∘cot267∘−sin223∘−sin267∘−cot267∘ is equal to
View Solutionकिसी व्यंजक का मान ज्ञात करना सीखें
View Solutionव्यंजक का मान ज्ञात करना |Part-2#!#Practice Questions
View SolutionWhat is the value of (cos267∘−sin223∘)?
View SolutionTabular Delta = |{:((sin^(2)23^(@), sin^(2)67^(@), cos 180^(@))),((-sin^(2)67^(@), - sin^(2)23^(@), cos^(2)180^(@))),((cos180^(@), sin^(2)23^(@), sin^(2)67^(@))):}| =………..
View SolutionThe value of the determinant Δ=∣∣ ∣ ∣∣sin223∘ sin267∘ cos180∘−sin267∘ −sin223∘ −cos180∘cos180∘ sin223∘ sin267∘∣∣ ∣ ∣∣ is
View Solution
