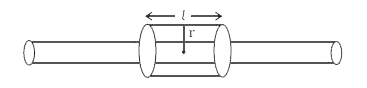
किसी $r_{0}$ त्रिज्या के अनन्त सिलिण्डर (बेलन) पर आवेश का रैखिक घनत्व - है। इसके समविभव के लिए समीकरण प्राप्त कीजिए।

Video Solution

Text Solution

Verified by Experts

The correct Answer is:नहीं

रेखा से दुरी r पर विभव ज्ञात करने के लिए विद्युत क्षेत्र पर विचार कीजिए। सममिति द्वारा हम यह पाते है कि क्षेत्र रेखाएँ बहिर्मुखी अरीय होनी चाहिए। त्रिज्या r तथा लम्बाई l का कोई गाउसीय पृष्ठ खीचिए। तब
$\oint E . d S = \frac{1}{ε_{0}} λ l$
अथवा $E_{r} 2 π r l = \frac{1}{ε_{0}} λ l$
$\Rightarrow E_{r} = \frac{λ}{2 π ε_{0} r}$
अतः यदि त्रिज्या $r_{0}$ है तब
$V (r) - V (r_{0}) = - \oint_{r_{0}}^{r} E . d l = \frac{λ}{2 π ε_{0}} ln \frac{r_{0}}{r}$
किसी दिए गए V के लिए,
$ln \frac{r}{r_{0}} = - \frac{2 π ε_{0}}{λ} = [V (r) - V (r_{0})]$
$\Rightarrow r = r_{0} e_{0}^{- 2 π ε_{0} V (r_{0}) / λ} . e_{0}^{+ 2 π ε_{0} V (r) / λ}$
समविभव पृष्ठ बेलनाकार है जिनकी त्रिज्या है
$\Rightarrow r = r_{0} e_{0}^{- 2 π ε_{0} [V (r) - V (r_{0})] λ}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR HINDI-स्थिर वैद्युत विभव तथा धारिता -दीर्घउत्तरीय (LA)

Home
Ask Doubt
Profile