वर्गीकृत आंकड़ों का माध्य अभिकलित करते समय, हम यह कल्पना करने हैं कि बारंबारताएं
सभी वर्गों में समान रूप से वितरित है
वर्गों के वर्ग चिन्हों पर केंद्रित है
वर्गों की उपरि सीमाओं पर केंद्रित है
2वर्गों की निम्न सीमाओं पर केंद्रित हैं
Step by step video & image solution for वर्गीकृत आंकड़ों का माध्य अभिकलित करते समय, हम यह कल्पना करने हैं कि बारंबारताएं by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सांख्यिकी और प्रायिकताBook:NCERT EXEMPLAR HINDIChapter:सांख्यिकी और प्रायिकताExercise:प्रश्नावली 13.2
Explore 14 Videos
- सांख्यिकी और प्रायिकताBook:NCERT EXEMPLAR HINDIChapter:सांख्यिकी और प्रायिकताExercise:प्रश्नावली 13.3
Explore 41 Videos
- सांख्यिकी और प्रायिकताBook:NCERT EXEMPLAR HINDIChapter:सांख्यिकी और प्रायिकताExercise:प्रश्नावली 13.4
Explore 12 Videos
- समांतर श्रेढ़ी Book:NCERT EXEMPLAR HINDIChapter:समांतर श्रेढ़ी Exercise:प्रश्नावली 5.4
Explore 12 Videos
Similar Questions
अवर्गीकृत आंकड़ों का माध्य तथा इन आंकड़ो को वर्गीकुत करने के बाद परिकलित किया गया माध्य सदैव बराबर होते है। क्या आप इस कथन से सहमत हैं? अपने उत्तर के लिए कारण दीजिए।
View Solutionनिम्नलिखित बंटन का माध्य ज्ञात कीजिएः

View Solutionनिम्नलिखित बंटन के लिए माध्य व प्रसरण ज्ञात कीजिए |
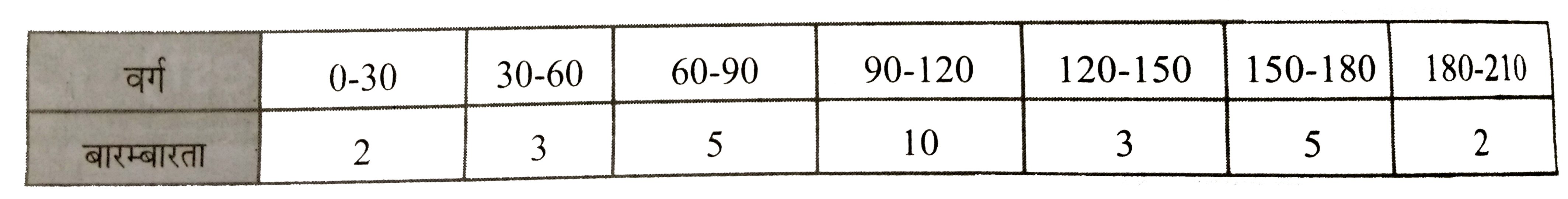
View Solutionकिसी AP के प्रथम पाँच पदों का योग और उसी AP के प्रथम सात पदों का योग का योग 167 है। यदि इस AP के प्रथम दस पदों का योग 235 है, तो इसके प्रथम 20 पदों का योग ज्ञात कीजिए।
View Solutionभूमिका | वर्गीकृत आकड़ों का माध्य | उदाहरण
View Solutionवर्गीकृत आंकड़ों का बहुलक | उदाहरण
View Solutionवर्गीकृत आंकड़ों का माध्यक | उदाहरण
View Solutionयदि निम्न बंटन का माध्य 50 है तो लुप्त बारंबारताएं ज्ञात कीजिए।

View Solutionवर्गीकृत आंकड़ों का माध्यक | उदाहरण (भाग -२)
View Solutionचलो देखते हैं दशमलव संख्याओं का भाग कैसे करते हैं ?
View Solutionश्वसन|हम स्वसन क्यों करते हैं
View SolutionBoards 2021|सांख्यिकी#!#वर्गीकृत आंकड़ों का बहुलक ज्ञात करना सीखे 45 Min में#!#Revision
View Solutionभूमिका|वर्गीकृत आकड़ों का माध्य
View Solution12वी प्री बोर्ड स्पेशल |नाभिकीय क्षय का माध्य समय
View Solutionवर्गीकृत आकड़ों के माध्य विचलन
View Solutionवर्गीकृत आंकड़ों की 'से कम प्रकार' और 'से अधिक प्रकर' की संचयी बारम्बारता वक्रों के प्रतिच्छेद बिन्दु के 'भुज' से प्राप्त होता है आंकड़ों का----
View Solution