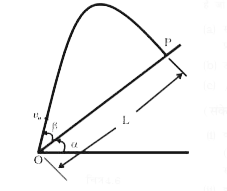
कोई कण वायु में किसी ऐसे समतल पृष्ठ से β कोण बनाते हुए प्रक्षेपित किया गया है जो स्वयं क्षैतिज से α कोण बनाता है (चित्र 4.6)।
(a) समतल पृष्ठ पर परास के लिए व्यंजक व्युत्पन्न कीजिए (समतल पृष्ठ पर प्रक्षेपण बिंदु से उस बिंदु तक की दूरी जहाँ प्रक्षेप्य जाकर टकराएगा)।
(b) उड्डगयन काल ज्ञात कीजिए।
(c) β का वह मान ज्ञात कीजिए जिस पर अधिकतम परास प्राप्त होगा।
यह समस्या दो भिन्न विधियों द्वारा हल की जा सकती है)।
(i) वह बिंदु Pजिस पर प्रक्षिप्त कण समतल से जाकर टकराता है उसे प्रक्षेप्य पथ (परवलय) तथा समतल के अनुदिश रेखा के कटान बिंदु के रूप में देखा जा सकता है। स्मरण रहे, कण क्षैतिज से कोण (α+β) पर प्रक्षिप्त किया गया है।
(ii) हम x-दिशा को समतल के अनुदिश और y-दिशा को इसके लंबवत् ले सकते हैं। तब इस प्रकरण में g (गुरुत्वीय त्वरण) को दो विभिन्न घटकों gx समतल के अनुदिश और gy इसके लंबवत् में नियोजित कीजिए। अब इस समस्या को क्रमश: x तथा y दिशाओं में समय को उभयनिष्ठ प्राचल के रूप में लेकर दो स्वतंत्र गतियों के रूप में हल किया जा सकता है।
Topper's Solved these Questions
- समतल में गति BOOK - NCERT EXEMPLAR HINDICHAPTER - समतल में गति EXERCISE - लघु उत्तरीय प्रश्न (SA)
8 Videos
- मात्रक और मापन BOOK - NCERT EXEMPLAR HINDICHAPTER - मात्रक और मापन EXERCISE - दीर्घ उत्तरीय प्रश्न (LA)
15 Videos
- सरल रेखा में गति BOOK - NCERT EXEMPLAR HINDICHAPTER - सरल रेखा में गति EXERCISE - दीर्घ उत्तरीय प्रश्न
10 Videos
Similar Questions
समतल सड़क पर, नियत वेग से, खुली कार में यात्रा करते हुए कोई लड़का किसी गेंद को वायु में ऊर्ध्वाधरतः ऊपर उछालता है और फिर उसे लपक लेता है। फुटपाथ पर खड़े किसी अन्य लड़के द्वारा प्रेक्षित गेंद की गति का आरेख खींचिए। अपने आरेख का स्पष्टीकरण कीजिए।
View Solutionमात्रकों की एक नई प्रणाली का प्रस्ताव किया गया है जिसके द्रव्यमान का मात्रक αkg, लंबाई का मात्रक βm तथा समय का मात्रक γs है। इस नई प्रणाली में 5 J का माप क्या होगा ?
View Solutionयह एक सामान्य प्रेक्षण है कि वर्षाधारी मेघ भूतल से लगभग 1km की ऊँचाई पर हो सकते हैं।
वर्षा की बुँदे यदि इतनी ऊँचाई से केवल गुरुत्व के अधीन गिरे तो भूतल पर पहुँचने पर इसकी चाल क्या होती ? इस मान km/h को में भी परिकलित कीजिए। (g=10m/s2)
View Solution2.0μC कोई बिंदु आवेश किसी किनारे पर 9.0 cm किनारे वाले किसी घनीय गॉउसीय पृष्ठ के केंद्र पर स्थिर है ? पृष्ठ से गुजरने वाला नेट फ्लक्स क्या है ?
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionबिन्दु (1,0,0) से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो XZ-समतल पर लम्ब है।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखाओ x=−3 तथा x=5 से समान दूरी पर है ।
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solutionएक सदिश ¯¯¯¯¯¯OA,OX से 60∘ का कोण बनाता है और OY से 45∘ का कोण बनाता है तथा ∣∣¯¯¯¯¯¯OA∣∣=10 इकाई है। बिंदु A का स्थिति सदिश ज्ञात कीजिए।
View Solutionउस समतल का समीकरण ज्ञात कीजिए, जो अक्षों से समान अन्तःखण्ड काटता है तथा बिंदु (2, 3, 4) से होकर जाता है |
View Solutionयदि बिंदु A(a,0) और B(−a,0) दो स्थिर बिंदु हों तो उस बिंदु का बिन्दुपथ ज्ञात कीजिए जिस पर रेखाखण्ड AB सदैव समकोण बनाता है ।
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसकी x-अक्ष से दूरी उसकी y-अक्ष से दूरी की तीन गुनी है ।
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसकी बिंदु (1, 2) से दूरी उसकी y-अक्ष से दूरी की दो गुनी है ।
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionमूल बिंदु से समतल 3x−4y+12z=3 की लम्ब दूरी ज्ञात कीजिए
View Solution
