किसी समतल में द्विविमीय गति का अध्ययन, स्थिति, वेग और त्वरण को। कार्तीय निर्देशांकों में सदिशों की भाँति A=Axˆi+Ayˆj के रूप में व्यक्त करके किया जा सकता है, यहाँ ˆi एवं ˆj क्रमशः x एवं y दिशा में एकांक सदिश है तथा Ax एवं Ay सदिश A के संगत घटक हैं। (चित्र 4.9)। गति का अध्ययन सदिशों को वृत्ताकार ध्रुवी निर्देशांकों के रूप में A=Arˆr+A0ˆθ की , rˆ=r/r=cosθiˆ+sinθj , ˆθ=−sinθˆi+cosθˆj उन दिशाओं में एकांक सदिश हैं जिनमें 'r' एवं 'θ' के मानों में वृद्धि हो रही है।
(a) ˆi एवं ˆj को r और θ के पदों में व्यक्त कीजिए। (b) दर्शाइए कि ˆr और ˆθ दोनों एकांक सदिश हैं और एक दूसरे के लंबवत् हैं।
(c) दर्शाइए कि ddt(ˆr)=ωˆ जहाँ ω=dθdt तथा ddt(ˆθ)=−ωˆr
(d) एक कण स्पाइरल (सर्पिल कुंडल) r=alphtaθˆr के अनुदिश गति करता है, यहाँ a= 1 है। इसके लिए 'a' की विमाएँ ज्ञात कीजिए।
(e) ऊपर (d) में वर्णित स्पाइरल के अनुदिश गति करते हुए कण के वेग एवं त्वरण ध्रुवी-सदिश निरूपण में ज्ञात कीजिए।
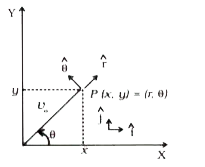
Step by step video & image solution for किसी समतल में द्विविमीय गति का अध्ययन, स्थिति, वेग और त्वरण को। कार्तीय निर्देशांकों में सदिशों की भाँति A=A_(x) hati+A_(y) hatj के रूप में व्यक्त करके किया जा सकता है, यहाँ hati एवं hatj क्रमशः x एवं y दिशा में एकांक सदिश है तथा A_(x) एवं A_(y) सदिश A के संगत घटक हैं। (चित्र 4.9)। गति का अध्ययन सदिशों को वृत्ताकार ध्रुवी निर्देशांकों के रूप में A=A_(r) hatr+A_(0) hat theta की , rˆ=r/r=cosθiˆ+sinθj , hat theta=- sin theta hati+cos theta hatj उन दिशाओं में एकांक सदिश हैं जिनमें 'r' एवं 'theta' के मानों में वृद्धि हो रही है। (a) hati एवं hatj को r और θ के पदों में व्यक्त कीजिए। (b) दर्शाइए कि hatr और hat theta दोनों एकांक सदिश हैं और एक दूसरे के लंबवत् हैं। (c) दर्शाइए कि (d)/(dt)( hatr)= omega hat जहाँ omega=(d theta)/(dt) तथा (d)/(dt) (hat theta)=- omega hat r (d) एक कण स्पाइरल (सर्पिल कुंडल) r= alphta theta hat r के अनुदिश गति करता है, यहाँ a= 1 है। इसके लिए 'a' की विमाएँ ज्ञात कीजिए। (e) ऊपर (d) में वर्णित स्पाइरल के अनुदिश गति करते हुए कण के वेग एवं त्वरण ध्रुवी-सदिश निरूपण में ज्ञात कीजिए। by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- समतल में गति BOOK - NCERT EXEMPLAR HINDICHAPTER - समतल में गति EXERCISE - लघु उत्तरीय प्रश्न (SA)
8 Videos
- मात्रक और मापन BOOK - NCERT EXEMPLAR HINDICHAPTER - मात्रक और मापन EXERCISE - दीर्घ उत्तरीय प्रश्न (LA)
15 Videos
- सरल रेखा में गति BOOK - NCERT EXEMPLAR HINDICHAPTER - सरल रेखा में गति EXERCISE - दीर्घ उत्तरीय प्रश्न
10 Videos
Similar Questions
समतल सड़क पर, नियत वेग से, खुली कार में यात्रा करते हुए कोई लड़का किसी गेंद को वायु में ऊर्ध्वाधरतः ऊपर उछालता है और फिर उसे लपक लेता है। फुटपाथ पर खड़े किसी अन्य लड़के द्वारा प्रेक्षित गेंद की गति का आरेख खींचिए। अपने आरेख का स्पष्टीकरण कीजिए।
View Solutionमात्रकों की एक नई प्रणाली का प्रस्ताव किया गया है जिसके द्रव्यमान का मात्रक αkg, लंबाई का मात्रक βm तथा समय का मात्रक γs है। इस नई प्रणाली में 5 J का माप क्या होगा ?
View Solutionयह एक सामान्य प्रेक्षण है कि वर्षाधारी मेघ भूतल से लगभग 1km की ऊँचाई पर हो सकते हैं।
वर्षा की बुँदे यदि इतनी ऊँचाई से केवल गुरुत्व के अधीन गिरे तो भूतल पर पहुँचने पर इसकी चाल क्या होती ? इस मान km/h को में भी परिकलित कीजिए। (g=10m/s2)
View SolutionThe component of vector A=axˆi+ayˆj+azˆk and the directioin of ˆi−ˆj is
View Solutionदो बिंदुओं P और Q के स्थिति सदिश क्रमशः 2¯a+¯b और ¯a−2¯b है। एक बिंदु R का स्थिति सदिश ज्ञात कीजिए जो रेखा खण्ड PQ को 1:2 के अनुपात में अंतः तथा बाहृातः विभाजित करता है।
View Solutionबिंदुओं P और Q के निर्देशांक निम्नानुसार है:
P(5,−7),Q(−3,2)
प्रत्येक स्थिति में सदिश ¯¯¯¯¯¯PQ को एकांक सदिशों ¯i और ¯j के पदों में व्यक्त कीजिए तथा ∣∣¯¯¯¯¯¯PQ∣∣ की गणना कीजिए।
View Solutionयदि बिंदु A जिसका स्थिति सदिश ¯a+2¯b है तथा सदिश ¯a,AB को 2:3 के अनुपात में विभाजित करता है तो B का स्थिति सदिश है:
View Solutionकिसी समतल में गति | किसी समतल में एक समान त्वरण से गति | दो विमाओं में आपेक्षिक वेग
View Solutionमाना R3 में p, q और r तीन असमतलीय सदिश हैं। माना सदिश s के घटक क्रमागत सदिशों p, q एवंr के अनुदिश क्रमशः 4, 3 और 5 हैं। यदि s के घटक क्रमागत सदिशों (−p+q+r),(p−q+r) एवं (−p−q+r) के अनुदिश क्रमशः x,y और z हैं, तब 2x+y+z का मान है।
View SolutionThe component of vector vecA = a_(x) hati+ a_(y) hatj + a_(z) hatk along th direction of (hati - hatj) is
View Solutionभोजन के रूप में पादपों के भाग #!#एवं जन्तु उत्पाद
View Solutionयदि किसी निश्चित कूट भाषा में "HAMMER" को "MAHERM" के रूप में लिखा जा सकता है तो उसी कूट भाषा में "MATTER" को किस प्रकार लिखा जाएगा?
View SolutionThe component of vector vecA=a_(x)hati+a_(y)hatj+a_(z)hatk along the direction of (hati-hatj) is
View SolutionThe component of vector A=axˆi+ayˆj+azˆk and the directioin of ˆi−ˆj is
View SolutionIn a certain code language, U is written as A, A as G, D as I, N as T, B as R, E as D and C as U. How will ABUNDANCE be written in that code? एक निश्चित कोड भाषा में,U को A के रूप में, A को G के रूप में, D को I के रूप में, N को T के रूप में, B को R के रूप में, E को D के रूप में, और C के रूप में लिखा जाता है। उस कोड में ABUNDANCE कैसे लिखा जाएगा?
View SolutionRevision |संगामी सदिश|शून्य सदिश|एकांक सदिश|सदिश निरूपण|सदिशों को घटको में तोड़ना|OMR|Summary
View Solution
