एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार पर और एक ही समांतर रेखाओ के बीच स्थित है, तो त्रिभुज के क्षेत्रफल का समांतर चतुर्भुज के क्षेत्रफल से अनुपात है
1:3
1:2
3:1
1:4
The correct Answer is:B
Step by step video & image solution for एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार पर और एक ही समांतर रेखाओ के बीच स्थित है, तो त्रिभुज के क्षेत्रफल का समांतर चतुर्भुज के क्षेत्रफल से अनुपात है by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NCERT EXEMPLAR HINDICHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.2 (सत्य और असत्य)
5 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NCERT EXEMPLAR HINDICHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.3
9 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NCERT EXEMPLAR HINDICHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.4
10 Videos
- संख्या पद्धतियाँBOOK - NCERT EXEMPLAR HINDICHAPTER - संख्या पद्धतियाँEXERCISE - प्रश्नावली 1.4
7 Videos
- सांख्यिकी और प्रायिकताBOOK - NCERT EXEMPLAR HINDICHAPTER - सांख्यिकी और प्रायिकताEXERCISE - प्रश्नावली (14.4)
12 Videos
Similar Questions
ABCD एक समान्तर चतुर्भुज और X भुजा AB का मध्य-बिंदु है । यदि ar(AXCD)=24cm2 है, तो ar(ABC)=24cm2 है।
View Solutionआकृति में, PSDA एक समांतर चतुर्भुज है। PS पर बिंदु Q और R इस प्रकार लिए गए है कि PQ=QR=RS है। तथा PA||QB||RC है। सिद्ध कीजिए कि ar (PQE) = ar (CFD) है।
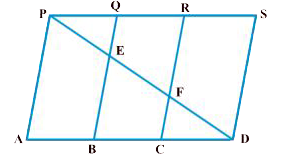
View Solutionकिसी समांतर चतुर्भुज ABCD की भुजा BC पर कोई बिंदु E लिया जाता है। AE और DC को बढ़ाया जाता है जिससे वे F पर मिलती है। सिद्ध कीजिए कि ar (ADF)=ar(ABFC) है।
View Solution0.6+0.¯7+0.4¯7 को pq के रूप में व्यक्त कीजिए , जहाँ p और q पूर्णांक हैं तथा q≠0 है।
View Solution60 विद्यार्थियों के गणित में (100 में से) प्राप्त किए गए अंक निम्नलिखित हैं :
16,13,5,80,86,7,51,48,24,56,70, 19,61,17,16,36,34,42,34,35,72,55,75,
31,52,28,72,97,74,45,62,68,86,35, 85,36,81,75,55, 26,95,31,7,78,92,62,
52, 56,15,63,25,36,54,44,47,27,72,17,4, 30.
वर्ग (0 - 9 से प्रारंभ करते हुए और प्रत्येक वर्ग की चौड़ाई 10 रखते हुए, एक वर्गीकृत बारंबारता बंटन सारणी बनाइए।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल |एक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|NCERT प्रश्नावली|सारांश
View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल |एक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|अभ्यास कार्य|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|NCERT प्रश्नावली|सारांश
View Solutionसमांतर चतुर्भुज के क्षेत्रफल पर आधारित महत्वपूर्ण प्रश्न
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|NCERT प्रश्नावली|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज|प्रमेय|अभ्यास कार्य|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|NCERT प्रश्नावली|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|NCERT प्रश्नावली|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|NCERT प्रश्नावली|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|NCERT प्रश्नावली|सारांश
View Solution
