X और Y त्रिभुज LMN की भुजा LN पर स्थित दो बिंदु इस प्रकार है कि LX=XY=YN है। X से होकर जाती हुई एक रेखा LM के समांतर खींची गई जो MN को Z पर मिलती है। सिद्ध कीजिए कि ar (LZY) = ar (MZYX) है।
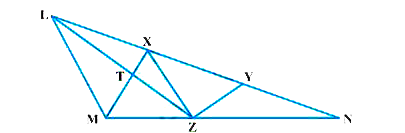
Step by step video & image solution for X और Y त्रिभुज LMN की भुजा LN पर स्थित दो बिंदु इस प्रकार है कि LX=XY=YN है। X से होकर जाती हुई एक रेखा LM के समांतर खींची गई जो MN को Z पर मिलती है। सिद्ध कीजिए कि ar (LZY) = ar (MZYX) है। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NCERT EXEMPLAR HINDICHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.4
10 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NCERT EXEMPLAR HINDICHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.2 (सत्य और असत्य)
5 Videos
- संख्या पद्धतियाँBOOK - NCERT EXEMPLAR HINDICHAPTER - संख्या पद्धतियाँEXERCISE - प्रश्नावली 1.4
7 Videos
- सांख्यिकी और प्रायिकताBOOK - NCERT EXEMPLAR HINDICHAPTER - सांख्यिकी और प्रायिकताEXERCISE - प्रश्नावली (14.4)
12 Videos
Similar Questions
किसी समांतर चतुर्भुज ABCD की भुजा BC पर कोई बिंदु E लिया जाता है। AE और DC को बढ़ाया जाता है जिससे वे F पर मिलती है। सिद्ध कीजिए कि ar (ADF)=ar(ABFC) है।
View SolutionABCD एक समान्तर चतुर्भुज और X भुजा AB का मध्य-बिंदु है । यदि ar(AXCD)=24cm2 है, तो ar(ABC)=24cm2 है।
View Solution0.6+0.¯7+0.4¯7 को pq के रूप में व्यक्त कीजिए , जहाँ p और q पूर्णांक हैं तथा q≠0 है।
View Solution60 विद्यार्थियों के गणित में (100 में से) प्राप्त किए गए अंक निम्नलिखित हैं :
16,13,5,80,86,7,51,48,24,56,70, 19,61,17,16,36,34,42,34,35,72,55,75,
31,52,28,72,97,74,45,62,68,86,35, 85,36,81,75,55, 26,95,31,7,78,92,62,
52, 56,15,63,25,36,54,44,47,27,72,17,4, 30.
वर्ग (0 - 9 से प्रारंभ करते हुए और प्रत्येक वर्ग की चौड़ाई 10 रखते हुए, एक वर्गीकृत बारंबारता बंटन सारणी बनाइए।
View SolutionX and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (see figure). Prove that ar(ΔLZY)=ar(MZYX).
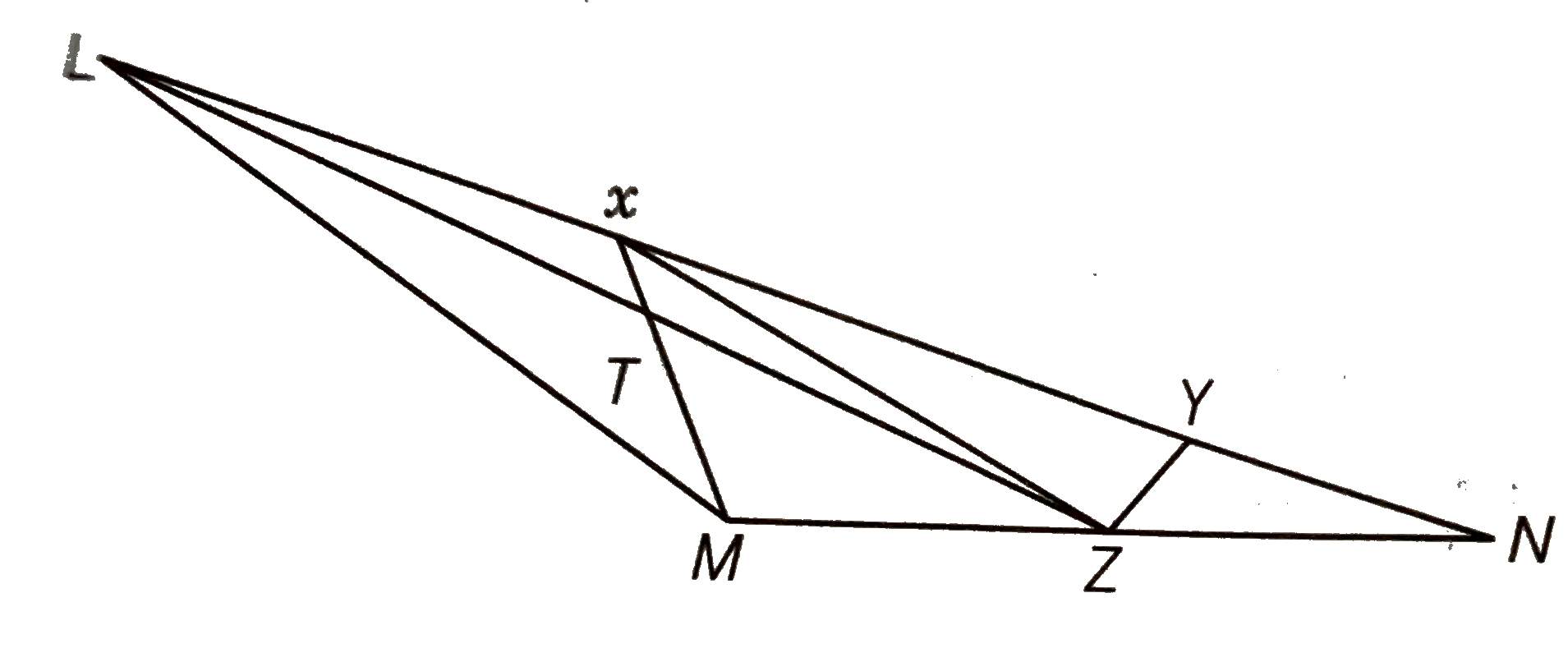
View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionउस रेखा के समीकरण ज्ञात कीजिए जो बिंदु (−1,3,2) से होकर जाती है तथा रेखाओं x1=y2=z3 और x+2−3=y−12=z+15 पर लम्ब है।
View Solutionसरल रेखा x−12=y−21=z+3−3 के समांतर उस रेखा के समीकरण ज्ञात कीजिए जो मूल बिंदु से होकर जाती है।
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है और y -अक्ष से ऐसा अन्तः खण्ड काटती है जो कि x -अक्ष पर काटे अन्तः खण्ड को दो गुना है।
View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionवृत्त x2+y2=4 के बिंदु (√3,1) पर खींची गई स्पर्श रेखा और अभिलम्ब तथा X-अक्ष एक त्रिभुज बनाते है । इस त्रिभुज का (वर्ग इकाइयो में) क्षेत्रफल है
View Solution
