दो उपग्रहों की त्रिज्याएं क्रमशः R1 एवं R2 हैं तथा उनके घनत्व क्रमश: ρ1 एवं ρ2 हैं। उनकी सतहों पर गुरुत्वीय त्वरण (g1/g2) का अनुपात होगा-
R1ρ2R2ρ1
R1ρ1R2ρ2
ρ1R22ρ2R21
R1R2ρ1ρ2
The correct Answer is:B
g=GMR2=GR243πR3ρ=43πGRρ
इसलिए g1g2=R1ρ1R2ρ2
Topper's Solved these Questions
- अभ्यास प्रश्न पत्र BOOK - NCERT FINGERTIPS HINDICHAPTER - अभ्यास प्रश्न पत्र EXERCISE - प्रश्न
50 Videos
- अभ्यास प्रश्न -पत्र -1BOOK - NCERT FINGERTIPS HINDICHAPTER - अभ्यास प्रश्न -पत्र -1EXERCISE - प्रश्न
50 Videos
- अभ्यास प्रश्न-पत्र - 3 BOOK - NCERT FINGERTIPS HINDICHAPTER - अभ्यास प्रश्न-पत्र - 3 EXERCISE - बहुविकल्पीय प्रश्न
50 Videos
Similar Questions
बल F को इस प्रकार दिया जाता है F=at+bt2, जहाँ t समय है, तो a एवं b की विमाएँ हैं
View Solution(चुम्बकीय आघूण )/( कोणीय संवेग ) की विमाएं हैं
View Solutionयदि E,M, J एवं G क्रमश: ऊर्जा, द्रव्यमान, कोणीय संवेग एवं गुरुत्वीय नियतांक को दर्शाते हैं, तो EJ2M5G2 किसकी विमाएं हैं?
View SolutionIf G_(1) and G_(2) are two geometric means and A is the arithmetic mean inserted two numbers,G_(1)^(2) then the value of (G_(1)^(2))/(G_(2))+(G_(2)^(2))/(G_(1)) is:
View SolutionThree planets of same density have radii R_(1),R_(2) and R_(3) such that R_(1) = 2R_(2) = 3R_(3) . The gravitational field at their respective surfaces are g_(1), g_(2) and g_(3) and escape velocities from their surfeces are upsilon_(1),upsilon_(2) and upsilon_(3) , then
View SolutionTwo planets have the same average density but their radii are R1 and R2. If acceleration due to gravity on these planets be g1 and g2 respectively, then
View Solutionयदि दो ग्रहो की त्रिज्यायें R1 व R2 हो तथा माध्य घनत्व ρ1 व ρ2 हो, तो सिद्ध कीजिए कि उन पर गुरुत्वीय त्वरणों का अनुपात R1ρ1:R2ρ2 होगा।
View Solutionदो ग्रहों के औसत घनत्व समान हैं परन्तु त्रिज्याएँ R1 तथा R2 हैं। यदि इन ग्रहों पर गुरुत्वीय त्वरण क्रमश: g1 तथा g2 हों, तो g1g2 होगा
View Solutionमाना कि X={1,2,3,4,5,6,7,8,9}, माना कि X में सम्बन्ध R1 तथा R2 इस प्रकार हैं कि R1={(x,y):x−y,3 से विभाज्य हैं,x≠y} तथा R2={(x,y):{x,y}⊂{1,4,7} या {x,y}⊂{2,5,8} या {x,y}⊂{3,6,9} जहाँ ⊂ का अर्थ उपसमुच्चय से हैं| दिखाएं कि R1=R2
View Solutionयदि दो ग्रहों की त्रिज्याएँ r1 तथा r2 व घनत्व d1 और d2, तथा गुरुत्वीय त्वरण g1 और g2 हों, तो सिद्ध कीजिए कि -
g1g2=r1d1r2d2
View Solutionसमान्तर श्रेढियों में से प्रतिमक का प्रथम पद 1 है | तथा उनके सार्व अंतर् क्रमश 1, 2, 3,.......,p है | सिद्ध कीजिए की उनके nवें पाडोकं का योग
12[(n−1)p2+p(n+1)] होगा |
View SolutionThe radii of two planets are respectively R1andR2 and their densities are respectively ρ1andρ2. The ratio of the accelerations due to gravity (g1/g2) at their surfaces is:
View SolutionThe radii of two planets are respectively R1andR2 and their densities are respectively ρ1andρ2. The ratio of the accelerations due to gravity (g1/g2) at their surfaces is:
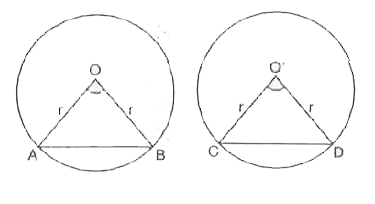
View Solutionआकृति में आपको दो वृत्त क्रमशः C(O, r) और C(O' r) दिए गए हैं| यदि उनकी संगत जीवाओं की लम्बाइयों में 1:1 का अनुपात हो तो उनके संगत केंद्रों में अंतरिक कोणों का अनुपात ज्ञात कीजिए |
View SolutionThree planets of same density have radii R1,R2 and R3 such that R1=2R2=3R3. The gravitational field at their respective surfaces are g1,g2 and g3 and escape velocities from their surfeces are υ1,υ2 and υ3, then
View SolutionTwo planets A and B have the same average density. Their radii RAandRB are such that RA:RB=3:1. If gAandgB are the acceleration due to gravity at the surfaces of the planets, the gA:gB equals
View Solution
