यदि वर्ग समीकरण 2x2−(a3+8a−1)x+a2−4a=0 के मूल विपरीत चिन्ह के हैं, तब
a≤0
0<a<4
4≤a<8
a≥8
The correct Answer is:B
Step by step video, text & image solution for यदि वर्ग समीकरण 2x^(2)-(a^(3)+8a-1)x+a^(2)-4a=0 के मूल विपरीत चिन्ह के हैं, तब by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - Solved Multiple Choice Questions (मूलों तथा गुणांकों के मध्य सम्बन्ध)58videos
वर्ग समीकरण एवं असमिकायें
- BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - Solved Multiple Choice Questions (मूलों के उभयनिष्ठ होने का प्रतिबंध, वर्ग व्यंजक व मूलों की स्थिति)18videos
वर्ग समीकरण एवं असमिकायें
- BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - JEE Advanced (Matrix Match type questions)2videos
वर्ग समीकरण एवं असमिकायें
- BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - JEE Advanced (integer type questions)8videos
लघुगणक और आंशिक भिन्नें
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Integer type questions)20videos
वृत्त तथा वृत्तों का निकाय
Similar Questions
यदि α तथा β समीकरण 4x2+3x+7=0 के मूल हों, तो 1α+1β=
If α and β are roots of 4x2+3x+7=0 then value of 1α+1β= is04:10View Solutionयदि दो समीकरणों x2−cx+d=0 तथा x2−ax+b=0 का एक उभयनिष्ठ मूल हो तथा दूसरा समीकरण समान मूल रखता है, तब 2(b+d)=
04:10View Solution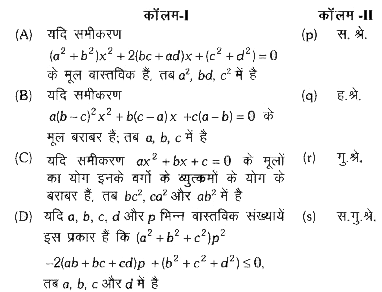
05:08View Solutionपद 6+log32⎛⎜ ⎜⎝13√2 ⎷4−13√2 ⎷4−13√2√4−13√2…⎞⎟ ⎟⎠ का मान है
02:22View Solutionरेखा 2x−3y=1 वृत्तीय क्षेत्र x2+y2≤6 को दो भागों में विभाजित करती है। यदि
S={(2,34),(52,34),(14,−14),(18,14)}, तो S में स्थित उन बिन्दुओं की संख्या जो लघुत्तर भाग में अन्दर है, निम्न है03:45View Solutionयदि समीकरण x2+px+q=0 के मूल, α,β है और समीकरण x2−rx+s=0 के मूल α4,β4 है, तो समीकरण x2−4qx+2q2−r=0 के सदैव
02:54View Solutionयदि α और β(α<β), समीकरण x2+bx+c=0 के मूल है, जहाँ c<0<b, तब
04:04View Solutionमाना समीकरण x2−x+p=0 के मूल α,β हैं और समीकरण x2−4x+q=0 के मूल γ,δ हैं। यदि α,β,γ,δ गुणोत्तर श्रेढ़ी में हैं, तब p और q के पूर्णांक मान (integer value) क्रमश: होंगे -
03:21View Solutionयदि समीकरण के Ax2+Bx+C=0 मूल α,β एव समीकरण x2+px+q=0 के α2,β2 हो तो p का मान है।
03:18View Solutionयदि समीकरण x2−bxax−c=m−1m+1 के मूल बारबार व् विपरीत चिन्हो के हो, तो m का मान होगा
02:51View Solutionयदि समीकरण x3−3x+2=0 के दो मूल बराबर हो, तो मूल होंगे।
03:13View Solutionयदि α,β समीकरण x2−3x+1=0 के मूल, हो तो वह समीकरण जिसके 1α−2,1β−2 मूल है, होगी।
02:57View Solutionयदि α,β द्विघात समीकरण x2+px+p3=0(p≠0) के मूल हो तथा (α,β) परवलय y2=x पर स्थित एक बिंदु हो, तो समीकरण के मूल होगा
03:46View Solutionयदि समीकरण x2−px+q=0 के मूल secα व cosecα है, तब
05:39View Solutionयदि समीकरण (a2+4a+3)x2+(a2−a−2)x+a(a+1)=0 के दो से अधिक मूल हैं, तो a का मान है
05:58View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
39:26View Solution