एक त्रिभुज के शीर्ष (cosα,sinα),(sinα,cosα) तथा मूल बिन्दु है। यदि त्रिभुज का क्षेत्रफल sin2α हो, तो α का मान है -
30∘
45∘
60∘
120∘
The correct Answer is:A
Step by step video, text & image solution for एक त्रिभुज के शीर्ष ("cos"alpha, "sin"alpha), ("sin"alpha, "cosalpha) तथा मूल बिन्दु है। यदि त्रिभुज का क्षेत्रफल "sin"^(2)alpha हो, तो alpha का मान है - by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
एक वर्ग का क्षेत्रफल एक आयत के क्षेत्रफल के बराबर है। यदि आयत की लम्बाई 16 मी और चौड़ाई 9 मी है, तो वर्ग की परिमिति निकालें -
01:13View Solutionनिम्न चित्र में छायांकित भाग का क्षेत्रफल है-
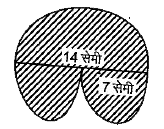 01:31View Solution
01:31View SolutionIf A=[[cosalpha, -sin alpha] , [sin alpha, cos alpha]] then A+A'=I then alpha=
04:19View SolutionIf A=[[cosalpha, sin alpha] , [-sin alpha, cos alpha]] and A^(-1)=A' then alpha=
03:50View Solutionयदि A=[cosαsinαsinαcosα] तो ज्ञात कीजिए 2A' और AA'
04:35View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
05:00View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
04:55View Solutionयदि समीकरण x2−2x+2=0 के मूल α तथा β हैं, तो n का न्यूनतम मान, जिसके लिए (αβ)n=1 है
04:32View Solutionयदि द्विघाती समीकरण, x2+xsinθ−2sinθ=0,θ∈(0,π2), के मूल α तथा β हैं , तो α12+β12(α−12+β−12).(α−β)24 बराबर है
03:50View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
04:48View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
03:51View Solutionयदि z−αz+α(α∈R) एक शुद्ध रूप से काल्पनिक संख्या है तथा |z|=2 है तो α का एक मान है
03:15View Solutionजहाँ ∣∣α2−β2∣∣=74 जहाँ α,β समीकरण 2x2+7x+c=0 के मूल हो, तो c का मान है।
02:57View Solutionयदि tanα व् tanβ समीकरण x2−px+q=0 के मूल हो, तो sin2(α+β) का मान है
05:26View Solutionयदि समीकरण px2+qx+r=0 के मूल sinα व cosα हों, तो
02:09View SolutionEliminate α between the equations :
sin2αcosα=a3andcos2αsinα=b302:00View Solution

