दो सामान समान्तर चतुर्भुज के कटे हुए भाग ABCD तथा A’B’C’D’ लीजिये। इनकी सांगत भुजाएँ सामान है।
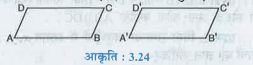 ¯¯¯¯¯¯¯¯A’B को ¯¯¯¯¯¯DC के ऊपर रखिए। क्या वे एक-दूसरे को पूर्णतया दकती है ? अब आप ¯¯¯¯¯¯AB और ¯¯¯¯¯¯DC की लम्बाई के बारे में क्या कह सकते हैं?
¯¯¯¯¯¯¯¯A’B को ¯¯¯¯¯¯DC के ऊपर रखिए। क्या वे एक-दूसरे को पूर्णतया दकती है ? अब आप ¯¯¯¯¯¯AB और ¯¯¯¯¯¯DC की लम्बाई के बारे में क्या कह सकते हैं?
Step by step video & image solution for दो सामान समान्तर चतुर्भुज के कटे हुए भाग ABCD तथा A^’ B^’ C^’ D^’ लीजिये। इनकी सांगत भुजाएँ सामान है। overline (A^’ B) को overline (DC) के ऊपर रखिए। क्या वे एक-दूसरे को पूर्णतया दकती है ? अब आप overline (AB) और overline (DC) की लम्बाई के बारे में क्या कह सकते हैं? by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
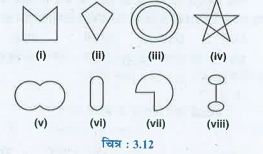
यहाँ पर कुछ आकृतिया दी गयी है । प्रत्येक का वर्गीकरण निन्मलिखित आधार पर कीजिये - साधारण वक्र
View Solutionमान ज्ञात कीजिए- 3−2
View Solutionएक नगर के संलग्न मानचित्र को देखिए।
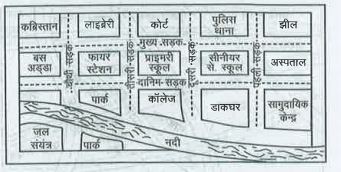 कॉलेज से झील तक के लिए एक छोटा सड़क का मार्ग गहरे गुलाबी रंग में खींचेए।
कॉलेज से झील तक के लिए एक छोटा सड़क का मार्ग गहरे गुलाबी रंग में खींचेए।
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionIn the following figure (not to scale) , ABCD is an isosecles trapezium. overline(AB)||overline(CD), AB=9cm and CD =12 CM, AP:PD =BQ:QC=1:2 . Find PQ.
View SolutionIn the figure, ¯¯¯¯¯¯RX⊥¯¯¯¯¯¯PA,¯¯¯¯¯¯RY⊥¯¯¯¯¯¯PB,RX=RY and ∠APR=70∘. Find ∠APQ
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E04_010_Q01.png" width="80%"gt
View SolutionIn the figure following, O is the centre of the circle and ¯¯¯¯¯¯AL⊥¯¯¯¯¯¯¯¯MN. If ∠AOB=90∘, then find ∠AOP
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E05_001_Q01.png" width="80%"gt
View SolutionThe value of ∣∣ ∣ ∣∣¯a⋅¯a¯a⋅¯b¯a⋅¯c¯b⋅¯a¯b⋅¯b¯b⋅¯c¯c⋅¯a¯c⋅¯b¯c⋅¯c∣∣ ∣ ∣∣=
View SolutionIf A, B, C, D, E are five coplanar points, then ¯¯¯¯¯¯DA+¯¯¯¯¯¯DB+¯¯¯¯¯¯DC+¯¯¯¯¯¯AE+¯¯¯¯¯¯BE+¯¯¯¯¯¯CE=
View SolutionIn parallelogram ABCD, if ¯¯¯¯¯¯AB=¯aand¯¯¯¯¯¯AD=¯b, then the diagonals interm of ¯aand¯b are
View SolutionABCDE is a pentagon. The resultant of the vectors ¯¯¯¯¯¯AB,¯¯¯¯¯¯AE,¯¯¯¯¯¯BC,¯¯¯¯¯¯DC,¯¯¯¯¯¯EDand¯¯¯¯¯¯AC in terms of ¯¯¯¯¯¯AC is
View SolutionIf ¯a⋅¯b=¯b⋅¯c=¯c⋅¯a=0, then ¯a⋅(¯bׯc)=
View Solution[¯a−¯b¯b−¯c¯c−¯a]=
View Solution[¯a+¯b¯b+¯c¯c+¯a]=
View Solution[¯a¯b+¯c¯c+¯b+¯a]=
View SolutionIf four points A(¯a),B(¯b),C(¯c)andD(¯d) are coplanar, then [¯a¯b¯d]+[¯b¯c¯d]+[¯c¯a¯d]=
View Solution
