किरण OA, OB, OC, OD और OE का एक सर्वानिष्ठ अंत बिंदु O है। तो दिखाइए कि ∠AOB+∠AOC+∠DOE+∠DOE+∠EOA=360∘
The correct Answer is:360∘
Step by step video, text & image solution for किरण OA, OB, OC, OD और OE का एक सर्वानिष्ठ अंत बिंदु O है। तो दिखाइए कि angleAOB+angleAOC+angleDOE+angleDOE+angleEOA=360^(@) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- रेखाएँ और कोण BOOK - KIRAN PUBLICATIONCHAPTER - रेखाएँ और कोण EXERCISE - EXERCISE - 8.1 (निम्न में कौन से कथन सत्य और कौन कथन असत्य है। )
5 Videos
- रेखाएँ और कोण BOOK - KIRAN PUBLICATIONCHAPTER - रेखाएँ और कोण EXERCISE - EXERCISE - 8.1 ( निम्नलिखित प्रश्नो के उत्तर दें। )
3 Videos
- यूक्लिड की ज्यामिति का परिचयBOOK - KIRAN PUBLICATIONCHAPTER - यूक्लिड की ज्यामिति का परिचयEXERCISE - EXERCISE 7.1
14 Videos
- लंबवृतीय बेलनBOOK - KIRAN PUBLICATIONCHAPTER - लंबवृतीय बेलनEXERCISE - EXERCISE-16
47 Videos
Similar Questions
रैखिक युग्म को बनाने वाले दोनों कोण न्यूनकोण होते है।
View Solutionयदि एक किरण किसी रेखा पर आधारित हो तो बने आसन्न कोण का योग कितना होगा ?
View Solutionनिम्नलिखित कथनों में से कौन-सा कथन सत्य है ?
View Solutionरिक्त स्थानों की पूर्ति करें।
एक लम्बवृतीय बेलन की त्रिज्या 7cm और ऊँचाई 5 cm हो, तो उसके वक्र पृष्ठ का क्षेत्रफल.....होगा।
View SolutionLet O be the centre of a regular hexagon ABCDEF. Find the sum of the vectors OA,OB,OC,OD,OE and OF
View SolutionOA = OBand OD = OC. Show that (i)ΔAOD≅ΔBOC and (ii)AD ∣∣ BC
View SolutionLet O be the centre of the regular hexagon ABCDEF then find −−→OA+−−→OB+−−→OD+−−→OC+−−→OE+−−→OF
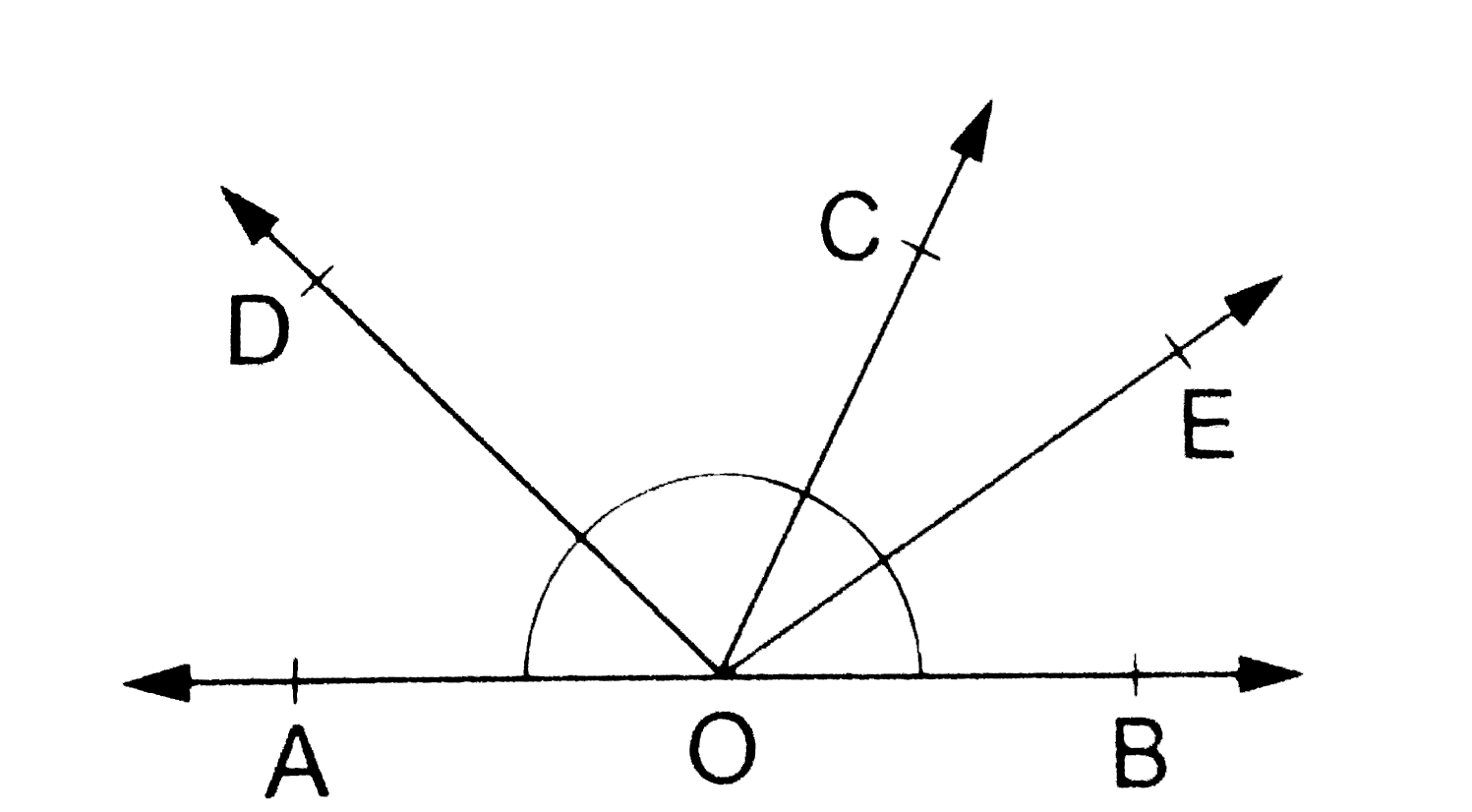
View SolutionIn the given figure, ray OC stands on a straight line AOB. Ray OD and ray OE are the bisectors of ∠AOC and ∠BOC respectively. Find the measure of ∠DOE.
View Solutionमाना कि O समष्टभुज ABCDEF का केंद्र हैं, तो
−−→OA+−−→OB+−−→OC=−−→OD+−−→OE+−−→OF.
View Solutionकिरणें OA,OB,OC,OD और OE का एक सर्वनिष्ठ अंत बिंदु O है। दिखायें कि ∠AOB+∠AOC+∠COD+∠DOE+∠EOA=360∘
View Solutionif D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABCandO be any points, then prove that OA+OB+OC=OD+OE+OF
View SolutionABCDE एक समपंचभुज है। O इसका केंद्र है। सिद्ध कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD+−−→OE=→0
View Solutionयदि ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b तथा C,AB पर एक ऐसा बिंदु है कि ¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB तो सदिश ¯¯¯¯¯¯OC बराबर है:
View SolutionIn given fig.
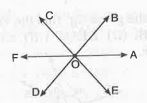 , Rays OA, OB, OC, OD and OE have common initial point O. Show that ∠AOB+∠BOC+∠COD+∠DOE+∠EOA=360∘.
, Rays OA, OB, OC, OD and OE have common initial point O. Show that ∠AOB+∠BOC+∠COD+∠DOE+∠EOA=360∘.
View Solutionबगल की आकृति में ∠AOB=90∘,OE,∠AOB का समद्विभाजक है, OC, ∠AOE का एवं OD, ∠EOB का समद्विभाजक है। तो क्या
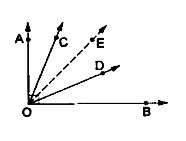
∠AOC≅∠COE≅∠EOD≅∠DOB
View Solutionबगल की आकृति में ∠AOB=90∘,OE,∠AOB का समद्विभाजक है, OC, ∠AOE का एवं OD, ∠EOB का समद्विभाजक है। तो क्या

∠AOC≅∠COE≅∠EOD≅∠DOB
View Solution
