sinAsinB=12[cos(A−B)]−cos(A+B) त्रिकोणमिति सम्बन्ध का उपयोग करके, हम cm(t)=Acsinωct+μAcsinωmtsinωct को निम्नलिखित प्रकार से लिख सकते हैं
cm(t)=Acsinωmt+μAc2cos(ωc−ωm)t−μAc2cos(ωc+ωm)t
cm(t)=Acsinωmt+μAc2cos(ωc−ωm)t−μAm2cos(ωc+ωm)t
cm(t)=Acsinωct+μAc2cos(ωc−ωm)t−μAc2cos(ωc+ωm)t
cm(t)=Acsinωct+μAc2cos(ωc−ωm)t−μAc2cos(ωc−ωm)t
The correct Answer is:C
त्रिकोणमितीय सम्बन्ध के उपयोग द्वारा
sinAsinB=12
[cos(A−B)−cos(A+B)]
हम लिख सकते हैं,
cm(t)=Acsinωct+μAcsinωmtsinωct
cm(t)=Acsinωct+μAc2
cos(ωc−ωm)t−μAc2(ωc+ωm)t
यहाँ, ωc−ωm तथा ωc+ωm को क्रमश: निम्न पार्श्व आवृत्ति तथा उच्च पार्श्व आवृत्ति कहते हैं।
Topper's Solved these Questions
- BOOK - NEET PREVIOUS YEARCHAPTER - संचार प्रणालीEXERCISE - Special Format वाले Objective प्रश्न ( I. कथन-कारण)7videos
संचार प्रणाली
- BOOK - NEET PREVIOUS YEARCHAPTER - संचार प्रणालीEXERCISE - Special Format वाले Objective प्रश्न (II. कथन प्रकार)8videos
संचार प्रणाली
- BOOK - NEET PREVIOUS YEARCHAPTER - संचार प्रणालीEXERCISE - NCERT पर based Objective प्रश्न (टॉपिक 3 विधुत चुम्बकीय तरंगों का संचरण)37videos
संचार प्रणाली
- BOOK - NEET PREVIOUS YEARCHAPTER - वुद्युत आवेश तथा क्षेत्र EXERCISE - MCQ29videos
वुद्युत आवेश तथा क्षेत्र
- BOOK - NEET PREVIOUS YEARCHAPTER - समतल की गति EXERCISE - MCQs35videos
समतल की गति
Similar Questions
एक विधि चित्र में ब्लॉक आरेख के रूप में दर्शाई गई है
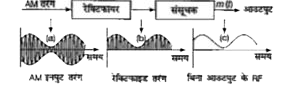 03:28View Solution
03:28View Solutionअंकिया सिगन्ल:
(i) मानों का संतत समुच्य प्रदान नहीं करते।
(ii) मानों को विविक्त चरणों के रूप में निरूपित करते है।
(iii) द्विआधारी पद्धति का उपयोग करते हैं।
(iv) दशमलव के साथ-साथ द्विआधारी पद्धति का भी उपयोग करते हैं।
उपरोक्त प्रकथनों में कौन-से सत्य हैं?
(a) केवल (i ) तथा (ii )
(b) केवल (ii ) तथा (iii )
(c ) (i) (ii) तथा (iii) परन्तु (iv ) नहीं13:09View Solutionजैसे-जैसे विधुत चुम्बकीय तरंगें प्रेषित्र से दूर होती जाती हैं, वैसे-वैसे इनकी तीव्रता
03:07View Solutionकोई इलेक्ट्रॉन विरामावस्था से किसी एकसमान तथा ऊपर की ओर निर्देशित ऊर्ध्वाधर विद्युत क्षेत्र E में दी गई दूरी h में गिरता है। अब, विद्युत क्षेत्र का परिमाण अपरिवर्तित रखते हुए इसकी दिशा उत्क्रमित (reverse) कर दी जाती है व किसी प्रोटॉन को विरामावस्था से इतनी ही ऊर्ध्वाधर दूरी h तक गिरने दिया जाता है। प्रोटॉन के गिरने में लिए गए समय की तुलना में इलेक्ट्रॉन द्वारा गिरने में लिया गया समय है
05:02View Solutionl लम्बाई की एक डोरी के एक सिरे में द्रव्यमान का एक कण जुड़ा है और इसका दूसरा एक चिमनी समतल मेज पर लगी छोटी - सी खूँटी से जुड़ा है , यदि यह कण वृत्ताकार पथ पर v चाल से घूर्णन करता है , यदि यह कण वृत्ताकार पथ पर चाल से घूर्णन करता है , तो उस पर लगने वाला नेट बल ( केंद्र की और ) ( जहाँ T रस्सी पर तनाव है )
01:37View SolutionIn sinA=sinB and cosA=cosB, then prove that sin(A−B)2=0
05:01View SolutionIf √2cosA=cosB+cos3B, and √2sinA=sinB−sin3B then sin(A−B)=
03:53View Solutionसर्वसमिकाओ को सिद्ध करो
sinA−sinBcosA+cosB+cosA−cosBsinA+sinB=008:57View Solutionसिद्ध कीजिए कि
cos(A−B)+sinA−cos(A+B)sin(A+B)+cosA−sin(A−B)=tanA.01:49View Solutionसिद्ध करें की (sinA⋅cosB+cosA⋅sinB)2+(cosA⋅cosB−sinA⋅sinB)2=1
02:32View Solutionसिद्ध करें की sin(B+A)+cos(B−A)sin(B−A)+cos(B+A)=cosA+sinAcosA−sinA
03:03View Solutionsin(A+B)=sinAcosB+cosAsinB
03:19View Solutionsin(A−B)=sinAcosB−cosAsinB
03:51View SolutionStatement-1 : sin(A+B)+sin(A−B)cos(A+B)+cos(A−B)=tanA
Statement-2 : sin(A+B)+sin(A−B)=sinA
and cos(A+B)+cos(A−B)=cosA.03:10View SolutionIn sinA=sinB and cosA=cosB, then prove that sin(A−B2)=0
View Solution

