Question

सिद्ध कीजिए :
किसी समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में बांटता है।

Explanation

मान लीजिए ABCD एक समांतर चतुर्भुज है और AC उसका एक विकर्ण है।



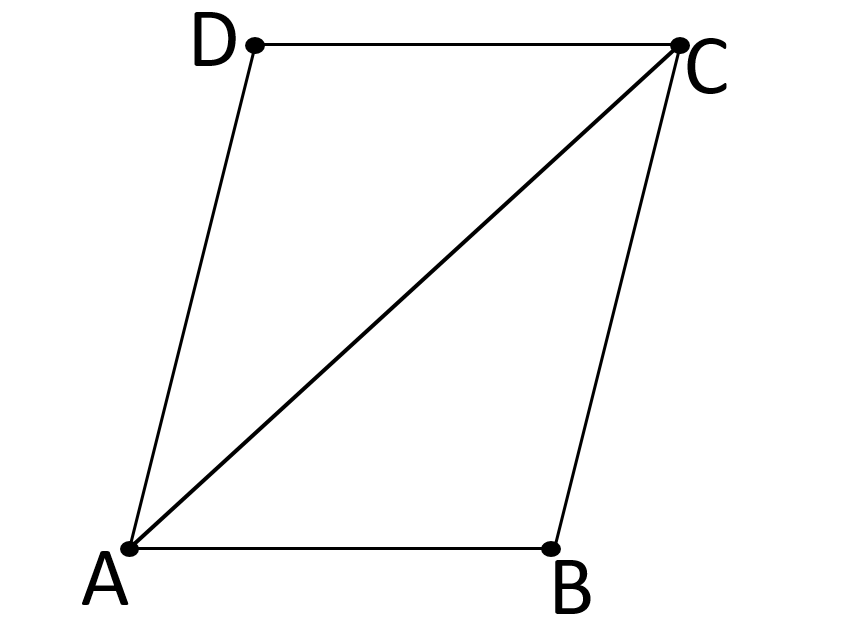
देखिए कि विकर्ण AC समांतर चतुर्भुज ABCD को दो त्रिभुजों ABC और CDA में विभाजित करता है।

हमें सिद्ध करना है कि ये दोनों त्रिभुज सर्वांगसम हैं। `(triangleABC cong triangleCDA)`

`triangleABC` और `triangleCDA` के लिए ध्यान दीजिए कि BC || AD है और AC एक तिर्यक रेखा है।

इसलिए, `angleBCA = angleDAC` (एकांतर कोण)

साथ ही, AB || DC और AC एक तिर्यक रेखा है।

इसलिए, `angleBAC = angleDCA` (एकांतर कोण)

और AC = CA ( उभयनिष्ठ भुजा )

अतः, `triangleABC cong triangleCDA` होगा |

अर्थात् विकर्ण AC समांतर चतुर्भुज ABCD को दो सर्वांगसम त्रिभुजों ABC और CDA में विभाजित करता हैं

अतः AB `= `DC और AD` =` DC होगा।