सिद्ध कीजिए :
एक समांतर चतुर्भुज में सम्मुख भुजाएँ बराबर होती है।
आप पहले ही सिद्ध कर चुके हैं कि समांतर चतुर्भुज का विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
अतः हम कह सकते हैं की समांतर चतुर्भुज कि सम्मुख भुजाएँ बराबर होंगी ।
इसलिए, AB = DC और AD = BC है।
( मान लीजिए ABCD एक समांतर चतुर्भुज है और AC उसका एक विकर्ण है।
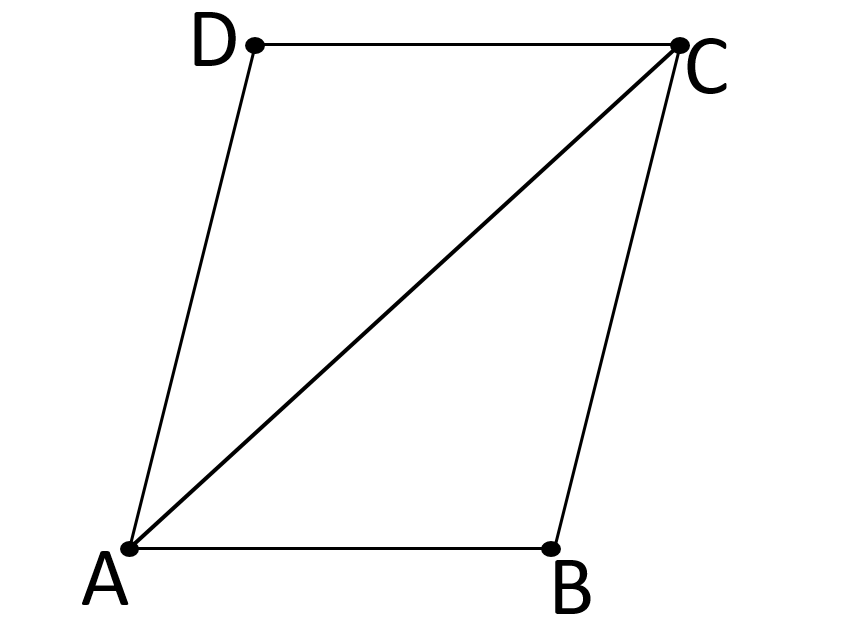
देखिए कि विकर्ण AC समांतर चतुर्भुज ABCD को दो त्रिभुजों ABC और CDA में विभाजित करता है।
हमें सिद्ध करना है कि AB = DC और AD = DC (△ABC≅△CDA)
△ABC और △CDA के लिए ध्यान दीजिए कि BC || AD है और AC एक तिर्यक रेखा है।
इसलिए, ∠BCA=∠DAC (एकांतर कोण)
साथ ही, AB || DC और AC एक तिर्यक रेखा है।
इसलिए, ∠BAC=∠DCA (एकांतर कोण)
और AC = CA ( उभयनिष्ठ भुजा )
अतः, △ABC≅△CDA होगा |
अर्थात् विकर्ण AC समांतर चतुर्भुज ABCD को दो सर्वांगसम त्रिभुजों ABC और CDA में विभाजित करता हैं
अतः AB = DC और AD = DC होगा।)

समान प्रश्न
सिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में ह्रासमान है ।
f(x)=sin4x+cos4x,x∈(0,π4)
View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में ह्रासमान है ।
f(x)=3x+5,x∈R,x≠0
View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में ह्रासमान है ।
f(x)=x2−2x+3,x<1
View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए हुए अन्तराल में ह्रासमान है -
f(x)=x2−2x+3,x<1
View Solutionसिद्ध कीजिए की फलन ,सम्मुख दिए गए अन्तराल में हास्यमान है।
f(x)=tan−1x−x,x∈R
View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक ही आधार और एक ही समांतर रेखाओं के बीच आकार्तियाँ#!#एक ही आधार और एक ही समांतर रेखाओ के बीच समांतर चतुर्भुज
View SolutionIf ABCD is a cyclic parallelogram , then the ∠A is .
यदि ABCD एक चक्रीय समांतर चतुर्भुज है, तो ∠A क्या है?
View Solution
