किसी 200 m ऊँची चट्टान के ऊपरी सिरे से दो पत्थरो को एक साथ क्रमशः 15ms−1 तथा 30ms−1 की प्रारंभिक चाल से ऊर्ध्वाधरतः ऊपर की ओर (vertically upward) फेंका जाता है। इस तथ्य का सत्यापन करे (verify ) कि चित्र 1.3 - 13 में प्रदर्शित ग्राफ पहले पत्थर के सापेक्ष दूसरे पत्थर कि आपेक्षिक स्थिति (relative position) का समय के साथ विचरण (variation) को सही रूप में व्यक्त करता है। (मान ले कि वायु प्रतिरोध नगण्य है और फर्श से टक्कर के बाद पत्थर तत्काल स्थिर हो जाते है , ऊपर कि ओर उछलते नहीं तथा g=10ms−2 ) ग्राफ के रेखीय (linear) एवं वक्रीय (curved) भागो के लिए समीकरण लिखे
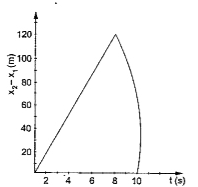
दो पत्थरो को जब भिन्न - भिन्न बेग से गुरुत्व के आधीन फेंका जाता है तब उनमे एक - दूसरे के लिए एकसमान आपेक्षिक चाल (uniform relative speed ) होती है तथा आपेक्षिक त्वरण शून्य होता है, क्योकि दोनों का त्वरण समान (अर्थात →g ) रहता है। ऐसी स्थिति में एक पत्थर के सापेक्ष दूसरे की गति सरल रेखा में होती है। इसे गणितीय विधि में भी प्रमाणित कर सकरे है -
समय t पर स्थिति को x(t) से तथा चाल को v(t) से व्यक्त करे, तो
सूत्र x(t)=x(0)=ut+12at2 से
पत्थर 1 के लिए x1(t)=200+15t−5t2 ...(1)
पत्थर 2 के लिए, x2(t)=200+30t−5t2 ...(2)
अब पत्थरो के बीच आपेक्षिक दुरी x2(t)−x1(t)=15 ...(3)
यह समीकरण t के पद में रैखिक संबंध (linear relation) व्यक्त करता है, अर्थात (x2−x1) एवं समय t के बीच ग्राफ सरल रेखा होगा
समीकरण (1) से, पत्थर का उड़ान - काल t1 ज्ञात करने के लिए x1(t)=0=200+15t−5t2
या 5t2−15t−200=0 या t2−3t−40=0 या (t−8)(t+5)=0∴t=8s
इसी प्रकार दूसरे पत्थर के लिए समीकरण (2) से
t2−6t−40=0 या (t−10)(t+4)=0,∴t1=10s
स्पष्टतः पत्थर 1 हवा में 8 s तक रहता है जबकि दूसरा पत्थर पहले पत्थर के जमीन पर आने के 2 s बाद जमीन पर आता है। दोनों पत्थरो के बीच आपेक्षिक दुरी का महत्तम मान समीकरण (3) से
x2−x1=15t=15×8=120m
पत्थर 2 की स्थिति 8 s से 10 s के बीच गुरुत्वाधीन त्वरित होगी जिसे चित्र 1 . 3 - 13 में वक्र द्वारा दिखाया गया है।
दोनों पत्थरो के बीच आपेक्षिक चाल
(=15ms−1) भी ग्राफ से
= महत्तम सापेक्षिक दुरी 8s=120m8s=15ms−1
इस प्रकार दिया गया ग्राफ निष्कर्षो की संतोषजनक व्याख्या करता है।
Topper's Solved these Questions
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.4 गति के नियम : घर्षण
33 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.5 कार्य , शक्ति और ऊर्जा
33 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.2 अदिश एवं सदिश
40 Videos
- सरल रेखा एवं समतल, में कण की गति BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)
24 Videos
Similar Questions
50 g द्रव्यमान का एक पत्थर ऊर्ध्वाधरतः ऊपर की ओर फेंका गया है। निम्नांकित परिस्थितियों के लिए पत्थर पर लग रहे नेट बल का परिमाण एवं दिशा बताए।
(a)ऊपर की ओर गति के क्रम में
(b) नीचे की ओर गति के क्रम में
(c) गति के उच्चतम बिंदु पर जहाँ पत्थर क्षणिक विराम (momentary rest) में रहता है
(d) विराम में स्थित रेलगाड़ी की खिड़की से पत्थर को गिराने के तुरंत बाद
View Solutionकिसी वस्तु पर आरोपित बल द्वारा किया गया कार्य धनात्मक अथवा ऋणात्मक दोनों हो सकता है नीचे दिए गए प्रकथनो को ध्यानपूर्वक पढ़कर करणसहित बताएँ कि निम्नांकित कार्य धनात्मक है अथवा ऋणात्मक ?
रस्से से बंधी किसी बाल्टी को रस्सी द्वारा कुएँ से बाहर निकलने में किसी व्यक्ति द्वारा किया गया कार्य
View Solutionयदि →a=3ˆi+4ˆj तथा →b=7ˆi+24ˆj तो वह सदिश ज्ञात करे जिसका परिमाण →b के तुल्य हो तथा दिशा →aके समांतर हो।
View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
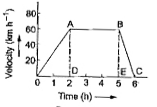
View Solutionयदि मूलबिंदु O के सापेक्ष त्रिभुज ABC के शीर्षों के स्थिति सदिश क्रमशः (1,−1,2),(2,1,3) और (−1,2,−1) है| तथा इसके केन्द्रक का स्थिति सदिश ज्ञात कीजिए|
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionकिसी कारखाने में बने एक बल्ब कि 150 दिनों के उपयोग के बाद फ्यूज होने कि प्रायिकता 0 .05 है प्रायिकता ज्ञात कीजिए कि इस प्रकार के 5 बल्बों में से - एक से अधिक
View Solution1 से 11 तक के पूर्णांकों में से यादृच्छया दो पूर्णांकों को चुना गया है | दोनों पूर्णांकों के विषय होने कि प्रायिकता ज्ञात करो यदि यह ज्ञात है कि दोनों पूर्णांकों का योग सम है |
View Solutionएक शतरंज प्रतियोगिता में m पुरुष तथा दो महिलाएं भाग ले रही है । प्रत्येक प्रतिभागी (participant) दूसरे प्रत्येक प्रतिभागी के साथ दो गेम खेलता है । यदि पुरुषो के बीच आपस में खेले गए गेमों कि संख्या, पुरुष तथा महिलाओ के बीच खेले गए गेमों की संख्या से 84 अधिक है , तो m का मान है
View Solution. किसी तथ्य की जानकारी हेतु प्रारंभिक प्राप्त प्रेक्षणों को किस प्रकार का आँकड़ा कहा जाता है?
View Solutionअध्ययन करके इस पर आधारित प्रश्नों के उत्तर दीजिए। शिक्षा केवल तभी बच्चों के आत्मिक जीवन का एक अंश बनती है, जबकि जान सक्रिय कार्यों के साथ अभिन्न रूप से जुड़ा हो। बच्चों से यह आशा नहीं की जा सकती कि पहाड़े या समकोण चतुर्भुज का क्षेत्रफल निकालने के नियम आप से आप उन्हें आकर्षित करेंगे। जब बच्चा यह देखता है कि ज्ञान सृजन के या श्रम के लक्ष्यों की प्राप्ति का साधन है, तभी वह ज्ञान पाने की इच्छा उनके मन में जागती है। मैं यह चेष्टा करता था कि छोटी आयु में ही शारीरिक श्रम में बच्चों को अपनी होशियारी और कुशाम बुद्धि का परिचय देने का अवसर मिले। स्कूल का एक सर्वाधिक महत्वपूर्ण कार्यभार है-बच्चों को ज्ञान का प्रयोग करना सिखाना। छोटी कक्षाओं में यह खतरा सबसे ज्यादा होता है कि शान निरर्थक बोझ बनकर रह जाएगा, क्योंकि इस आयु में बौद्धिक श्रम नई-नई बातें सीखने से ही सम्बन्धित होता है। लेखक के अनुसार शिक्षा का अर्थ है
View Solutionअध्ययन करके इस पर आधारित प्रश्नों के उत्तर दीजिए। शिक्षा केवल तभी बच्चों के आत्मिक जीवन का एक अंश बनती है, जबकि जान सक्रिय कार्यों के साथ अभिन्न रूप से जुड़ा हो। बच्चों से यह आशा नहीं की जा सकती कि पहाड़े या समकोण चतुर्भुज का क्षेत्रफल निकालने के नियम आप से आप उन्हें आकर्षित करेंगे। जब बच्चा यह देखता है कि ज्ञान सृजन के या श्रम के लक्ष्यों की प्राप्ति का साधन है, तभी वह ज्ञान पाने की इच्छा उनके मन में जागती है। मैं यह चेष्टा करता था कि छोटी आयु में ही शारीरिक श्रम में बच्चों को अपनी होशियारी और कुशाम बुद्धि का परिचय देने का अवसर मिले। स्कूल का एक सर्वाधिक महत्वपूर्ण कार्यभार है-बच्चों को ज्ञान का प्रयोग करना सिखाना। छोटी कक्षाओं में यह खतरा सबसे ज्यादा होता है कि शान निरर्थक बोझ बनकर रह जाएगा, क्योंकि इस आयु में बौद्धिक श्रम नई-नई बातें सीखने से ही सम्बन्धित होता है। ज्ञान-प्राप्ति की इच्छा कब जागती है?
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View SolutionFrom the top of a tower, the angles of depression of two objects on the ground on the same side of it, are observed to be 60^@ and 30^@ respectively and the distance between the objects is 400 sqrt3 m. The height (in m) of the tower is : किसी मीनार के शीर्ष से, भूमि पर इसके एक ही तरफ स्थित दो वस्तुओं का अवनमन कोण क्रमशः 60^@ और 30^@ पाया जाता है तथा वस्तुओं के बीच की दूरी 400 sqrt3 मीटर है | इस मीनार की ऊंचाई ( मीटर में ) है
View Solutionएक अवाष्पशील विलेय से युक्त जलीय विलयन के वाष्प दाब का आपेक्षिक अवनमन 0.0125 है। विलयन की मोललता है:
View Solutionएक alpha - कण, कॉपर के नाभिक (Z=29) के लक्ष्य की ओर इस प्रकार से उपगमन करता है। कि संघट्ट प्राचल का मान शून्य होता है। निकटतम उपगमन की दूरी होगी:
View Solution
