किसी कण की गति में इसका स्थिति सदिश (position vector) →r को समय t के फलन (function) के रूप में निम्नांकित संबंध द्वारा व्यक्त किया गया है।
→r=(3tˆi−2t2ˆj+4ˆk) m , जहाँ समय सेकंड में है तथा सभी गुणाको (coefficients) के मात्रक इस प्रकार से है कि →r का मात्रक मीटर रहे।
कण का →v तथा →a ज्ञात करे , तथा
कण का तात्क्षणिक वेग, →v=d→rdt तथा तात्क्षणिक त्वरण →a=d→vdt
प्रश्न से →r=(3tˆi−2t2ˆj+4ˆk)m
∴→v=d→rdt=ddt(3tˆi−2t2ˆj+4ˆk)ms−1
=3ˆi−4tˆjms−1
→a=d→vdt=ddt(3.0ˆi−4.0tˆj)ms−2
=−4.0ˆjms−2
Topper's Solved these Questions
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.4 गति के नियम : घर्षण
33 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.5 कार्य , शक्ति और ऊर्जा
33 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.2 अदिश एवं सदिश
40 Videos
- सरल रेखा एवं समतल, में कण की गति BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)
24 Videos
Similar Questions
50 g द्रव्यमान का एक पत्थर ऊर्ध्वाधरतः ऊपर की ओर फेंका गया है। निम्नांकित परिस्थितियों के लिए पत्थर पर लग रहे नेट बल का परिमाण एवं दिशा बताए।
(a)ऊपर की ओर गति के क्रम में
(b) नीचे की ओर गति के क्रम में
(c) गति के उच्चतम बिंदु पर जहाँ पत्थर क्षणिक विराम (momentary rest) में रहता है
(d) विराम में स्थित रेलगाड़ी की खिड़की से पत्थर को गिराने के तुरंत बाद
View Solutionकिसी वस्तु पर आरोपित बल द्वारा किया गया कार्य धनात्मक अथवा ऋणात्मक दोनों हो सकता है नीचे दिए गए प्रकथनो को ध्यानपूर्वक पढ़कर करणसहित बताएँ कि निम्नांकित कार्य धनात्मक है अथवा ऋणात्मक ?
रस्से से बंधी किसी बाल्टी को रस्सी द्वारा कुएँ से बाहर निकलने में किसी व्यक्ति द्वारा किया गया कार्य
View Solutionयदि →a=3ˆi+4ˆj तथा →b=7ˆi+24ˆj तो वह सदिश ज्ञात करे जिसका परिमाण →b के तुल्य हो तथा दिशा →aके समांतर हो।
View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
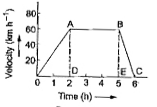
View SolutionFor any vector →r , prove that →r=(→r.ˆi)ˆi+(→r.ˆj)ˆj+(→r.ˆk)ˆk.
View SolutionIf →r.ˆi=→r.ˆj=→r.ˆkand|→r|=3, then find the vector →r.
View SolutionConsider a line vec r=hat i+t(hat i+hat j+hat k) and a plane (vec r-(hat i+hat j))*(hat i-hat j-hat k)=1
View SolutionFind the shortest distance between the given line
→r=(3−t)ˆi+(4+2t)ˆj+(t−2)ˆk
→r=(1+s)ˆi+(3s−7)ˆj+(2s−2)ˆk
View Solutionयदि →a=ˆi+ˆj+ˆk,→b=2ˆi−ˆj+3ˆk और →c=ˆi−2ˆj+ˆk तो सदिश 2→a−→b+3→c के समांतर एक मात्रक सदिश ज्ञात कीजिए ।
View Solutionदर्शाइए कि बिंदु A,B,C जिनके स्थिति सदिश क्रमशः →a=3ˆi−4ˆj−4ˆk,→b=2ˆi−ˆj+ˆk और →c=ˆi−3ˆj−5ˆk है एक समकोण त्रिभुज के शीर्ष है।
View Solutionसदिश →a+→b और →a−→b कि लम्ब दिशा में मात्रक सदिश ज्ञात कीजिए जहाँ →a=3ˆi+2ˆj+2ˆk और →b=ˆi+2ˆj−2ˆk है।
View Solutionबिन्दु (1,2,3) से जाने वाली तथा समतलो →r.(ˆi−ˆj+2ˆk)=5 और →r.(3ˆi+ˆj+ˆk)=6 के समान्तररेखा के सदिश समीकरण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए की रेखा →r=2ˆi−2ˆj+3ˆk+t(ˆi−ˆj+4ˆk) समतल →r.(ˆi+5ˆj+ˆk)=5 के समान्तर है उसके बीच की दूरी ज्ञात कीजिए।
View Solutionरेखाएं जिनकी सदिश समीकरण निम्नलिखित हैं , के बीच की न्यूनतम दूरी ज्ञात कीजिए-
→r=(1−t)ˆi+(t−2)ˆj+(3−2t)ˆk और →r=(s+1)ˆi+(2s−1)ˆj−(2s+1)ˆk
View Solutionदो रेखाओ जिनके सदिश समीकरण →r=(3−t)ˆi+(4−2t)ˆj+(t−2)ˆk तथा →r=(1+s)ˆi+(3s−7)ˆj+(2s−2)ˆk है , के बीच की न्यूनतम दूरी ज्ञात कीजिए।
View Solutionसमतलो →r.(ˆi−ˆj+ˆk)+3=0 तथा →r.(ˆi+2ˆj+k)−5=0के बीच का कोण है -
View Solution
