किसी सरल रेखा पर सरल आवर्त गति करते हुए कण की स्थितिज ऊर्जा U(x) को स्थिति x के फलन के रूप में U(x)=12kx2 से व्यक्त किया गया है , जहाँ दोलित्र का बल - नियतांक (force constant) k है। k=0.5Nm−1 के लिए U(x) एवं x के बीच विचरण (variation) को चित्र 1.5-1 में दिखया गया है। प्रमाणित कर कि 1जूल कि कुल ऊर्जा से युक्त किसी कण को ऐसे विभव के अधीन स्थिति x=±2m में अवश्य ही वापस आना चाहिए

सरल आवर्त गति में दोलित्र (oscillator ) की गति पर्त्यानयन बल F = - kx के अधीन होती है, जहाँ F= प्रत्यायन बल तथा x = माध्य स्थिति से विस्थापन
दोलित्र की कुल यांत्रिक ऊर्जा = = महत्तम स्थितिज ऊर्जा = महत्तम गतिज ऊर्जा
यदि दोलनि गति के विस्थापन का आयाम A हो तो
महत्तम स्थितिज ऊर्जा 12kA2=1 जूल
∴A=√2Jk=√2J0.5Nm−1=√2×2m2=2m
प्रकृति के नियमानुसार , स्थितीज ऊर्जा को न्यूनतम करने के लिए दोलित्र अवश्य वापस आएगा ओर स्थितिज ऊर्जा का रूपांतर गतिज ऊर्जा में होगा।
Topper's Solved these Questions
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.6 वृत्तीय गति
17 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.7 आवेग एवं संवेग
20 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.4 गति के नियम : घर्षण
33 Videos
- सरल रेखा एवं समतल, में कण की गति BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)
24 Videos
Similar Questions
1.5 m लंबी डोरी के एक सिरे पर किसी पत्थर को बाँधकर फर्श से 2m ऊँचाई पर क्षैतिज वृत्तीय पथ पर एकसमान चाल से घुमाया जाता है। गति के क्रम से डोरी के अचानक टूट जाने पर पत्थर प्रक्षेप्य गति करता हुआ 10 m की दुरी पर फर्श से टकराता है पत्थर की वृत्तीय गति में अभिकेंद्र त्वरण का मान ज्ञात करे।
View Solution1 kg तथा 16 kg द्रव्यमान के दो ब्लॉक की गतिज उर्जाएँ समान उनके रैखिक संवेग का अनुपात ज्ञात करे।
View Solution50 g द्रव्यमान का एक पत्थर ऊर्ध्वाधरतः ऊपर की ओर फेंका गया है। निम्नांकित परिस्थितियों के लिए पत्थर पर लग रहे नेट बल का परिमाण एवं दिशा बताए।
(a)ऊपर की ओर गति के क्रम में
(b) नीचे की ओर गति के क्रम में
(c) गति के उच्चतम बिंदु पर जहाँ पत्थर क्षणिक विराम (momentary rest) में रहता है
(d) विराम में स्थित रेलगाड़ी की खिड़की से पत्थर को गिराने के तुरंत बाद
View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
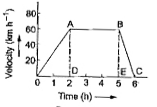
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionएक सरल रेखा द्वारा अक्षो के बीच काटे गये अन्तः खण्ड को बिंदु (7,9),3:1 के अनुपात में अन्तः विभाजित करता है रेखा का समीकरण ज्ञात कीजिए
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो मूलबिंदु से होकर जाती है और निर्देशाओं के बीच सरल रेखा 3x+y=12 के भाग को 1:2 के अनुपात में विभाजित करती है।
View Solutionकिसी सरल रेखा से अक्षों के बीच काटे हुए अन्तः खण्ड का मध्य-बिन्दु (3,-2) है। रेखा का समीकरण ज्ञात कीजिए।
View Solutionएक सरल रेखा बिन्दु (-1,5) से होकर जाती है और रेखा द्वारा अक्षो के बीच काटे हुए भाग को यह बिन्दु 3:2 के अनुपात में विभाजित करता है। रेखा का समीकरण ज्ञात कीजिए|
View Solutionc के उन मानों की संख्या जिनके लिए सरल रेखा y=4x+c वक्र x24+y2=1 को स्पर्श करती है, होगी
View Solutionवक्र y=ex,y=e−x तथा सरल रेखा x=1 के बीच घिरे क्षेत्र का क्षेत्रफल है।
View Solutionएक फलन g जो प्रत्येक वास्तविक संख्या x>0 के लिए परिभाषित है तथा g(1)=1,g'(x2)=x3 को सभी x>0 के लिए सन्तुष्ट करता है, तो g (4) का मान है
View Solutionc के उन मानों की संख्या जिनके लिए सरल रेखा y=4x + c वक्र x2/4+y2=1 को स्पर्श करती है, है
View Solutionदोलन|सरल आवर्त गति #!#स्प्रिंगब्लॉक निकाय के सरल आवर्त गति
View Solutionसरल आवर्त गति में ऊर्जा|स्प्रिंग के दोलन
View Solutionसरल रेखा के समीकरणों के विभिन्न रूप
View Solution
