किसी रुक्ष (rough) क्षैतिज समतल पर ऊर्ध्वाधरतः (vertically) स्थित लंबाई l का एकसमान (uniform) छड़ विराम से ऊर्ध्वाधर तल में गिरता है। यदि घर्षण पर्याप्त (sufficient) हो ताकि निचला सिरा नहीं फिसले , तो इसके मुक्त सिरे का रैखिक वेग (linear speed) ज्ञात करे जब यह
(i) ऊर्ध्वाधर से θ कोण बनाता हो
(ii) क्षैतिज तल से टकराता हो।
प्राम्भिक स्तिथि में छड़ का गुरुत्व केंद्र क्षैतिज तल से l2 ऊँचाई पर है तथा θ कोण से विक्षेपित होने पर (चित्र 1.8-11) यह ऊँचाई l2cosθ होगी। गुरुत्व केंद्र का नीचे की ओर विस्थापन
h=12−l2cosθ=l2(1−cosθ)
अतः , छड़ की स्थितिज ऊर्जा (potential energy) में ह्यस,
ΔPR=mgh=mg(l)2(1−cosθ) . . . (1)
स्थितिज ऊर्जा का यह ह्यस छड़ की घूर्णन गतिज ऊर्जा (rotational KE) में रूपांतरित होता है। यदि A. B स्थिति में इसकी कोणीय चाल ω हो, तो छड़ की गतिज ऊर्जा
=12Iω2 . . . (2)
∴12Iω2=mg(l)2(1−cosθ) . . . (3)
अब छड़ का जड़त्व-आघूर्ण B से गुजरने वाले क्षैतिज अक्ष के पारित: I=13ml2
, समीकरण (3) से 12,13ml2⋅ω2=mg(l)2(1−cosθ)
अतः, अभीष्ट कोणीय चाल ω=√3gl(1−cosθ)
क्षैतिज तल से टकराते समय θ=90∘,cosθ=0
अतः, टकराते समय कोणीय चाल =√3gl
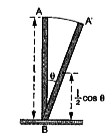
Topper's Solved these Questions
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1. 9 गुरुत्वाकर्षण25videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.10 प्रत्यास्थता27videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.7 आवेग एवं संवेग20videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)24videos
सरल रेखा एवं समतल, में कण की गति
Similar Questions
किसी विघुत आवेश को अन्य आवेशों के वैघुत बलों से परिरक्षित (shield ) करने के लिए उस आवेश को खोखले चालक के अंदर रखा जाता है । क्या किसी वस्तु को अन्य द्रव्यमान के गुरुत्वीय बलों से परिरक्षित करने के लिए उसे किसी खोखले गोले में रखकर या किसी अन्य साधन द्वारा ऐसा किया जा सकता है ?
09:03View Solutionदो पदार्थो A और B के लिए प्रतिबल - विकृति (stress-strain) ग्राफ चित्र 1.10-1 में दर्शाए गए है। इन ग्राफो को एक ही पैमाना (scale) मानकर खींचा गया है।
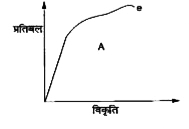
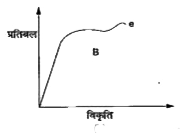
किस पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है ?04:21View Solution1 kg तथा 16 kg द्रव्यमान के दो ब्लॉक की गतिज उर्जाएँ समान उनके रैखिक संवेग का अनुपात ज्ञात करे।
05:05View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
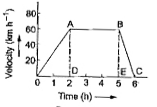
02:01View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?03:00View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
03:00View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
03:00View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
32:05View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3,4) और केन्द्र (2,3) हो, तो दूसरे सिरे के निर्देशांक ज्ञात कीजिए।
03:54View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3, 4) और केन्द्र (2,3) हो, तो दूसरे सिरे का निर्देशांक ज्ञात कीजिए।
01:52View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3, 4) और केन्द्र (2,3) हो, तो दूसरे सिरे का निर्देशांक ज्ञात कीजिए।
02:13View Solutionघर्षण कोण | समतल सतह पर वस्तु की गति | आनत तल पर वस्तु की गति
49:45View Solutionएक त्रिभुज का क्षेत्रफल 30 सेमी2 यदि ऊँचाई आधार से 7 ज्यादा हो, तो आधार ज्ञात करे |
42:51View Solutionयदि 4964A, 9 से विभाज्य है तो अंक A का मान क्या हो सकता है?
54:20View Solutionयदि किसी भिन्न का अंश, हर से 2 कम है और यदि हर में 1 जोडा जाए तो यह 12 हो जाता है तब वह भिन्न होगी ?
View Solutionएक कोण पर झुके हुए तल पर ऊँचाई से प्रक्षेप्य
View Solution