x-अक्ष के अनुदिश सरल आवर्त गति करते हुए किसी कण की तात्कालिक स्थिति को समय के फलन के रूप में निम्नांकित संबध द्वारा व्यक्त किया जाता है -
x(t)=acos(ωt+ϕ)
यदि प्रारंभ में (अर्थात t = 0 पर ) कण की स्थिति 1 cm पर तथा चाल ωcms−1 हो, तो कण के आयाम (amplitude) तथा प्रारंभिक कला - कोण (initial phase or epoch) ज्ञात करे। कण की कोणीय आवृत्ति (angular frequency) πs−1 है। यदि कण की तात्कालिक स्थिति को समीकरण (1) से व्यक्त cosine फलन के बदले sine फलन समीकरण (2) से व्यक्त किया जाए :
x(t)=Bsin(ωt+α)
तो प्रारंभिक प्रतिबंध (initial condition) समान रखते हुए कण के आयाम तथा प्रारंभिक कला - कोण ज्ञात करे।
प्रश्न से, x(t)=Acos(ωt+ϕ) . . . (1)
प्रारंभिक प्रतिबंध (t=0) के कारण,
जब t=0, तक x=1 cm
∴ समीकरण (1) से, 1 cm=Acos(ω×0+ϕ)=Acosϕ
∴Acosϕ=1 cm . . . (2)
समीकरण (1) का समय t के सापेक्ष अवकलन करने पर, तात्क्षणिक वेग,
v(t)=dx(t)dt=−Aωsin(ωt+ϕ) . . . .(3)
फिर, t=0 पर, v=ω cm s−1, अतः समीकरण (3) से,
ω cm s−1=−Aωsin(ω×0+ϕ)=−A(ω s−1)sinϕ
∴ A sinϕ=−1 cm . . . .(4)
समीकरण (2) तथा (4) के वर्ग के योगफल से,
A2cos2ϕ+A2sin2ϕ=(1 cm)2+(−1 cm)2=2 cm2.
अतः अभीष्ट आयाम, A=√2 cm.
अब समीकरण (4) को समीकरण (2) से भाग देने पर,
AsinϕAcosϕ=(−1 cm)(1 cm)=−1
या tanϕ=−1
∴ϕ=3π4 या ϕ=7π4.
अब निर्देश वृत्त के अनुसार ϕ=3π4 में विस्थापन x ऋणात्मक है लेकिन ϕ=7π4 के लिए x का मान धनात्मक है अतः, प्रारंभिक कला का अभीष्ट मान =7π4.
अब, यदि व्यक्त करने के लिए sine फलन प्रयुक्त हो, अर्थात
x=Bsin(ωt+α) . . . (5)
तब, वेग v=dxdt=ddt[Bsin(ωt+α)]=Bωcos(ωt+α) . . . (6)
अब, t=0 पर, x=1 cm तथा v=ω cm s−1 लेने पर
समीकरण (5) से, Bsinα=1 cm तथा समीकरण (6) से, Bcosα=1 cm.
अतः, अभीष्ट आयाम B=√2 cm.
फिर, BsinαBcosα=1 या tanα=1, ∴α=π4 या 5π4.
निर्देश वृत्त के अनुसार प्रारंभिक कला के π4 मान के लिए स्थिति (x) एवं वेग (v) दोनों आवश्यक शर्त के अनुसार धनात्मक है।
अतः, प्रारंभिक कला का अभीष्ट मान α=π4.
Topper's Solved these Questions
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.12 तरल दाब : पास्कल का नियम : पृष्ठ - तनाव19videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1 . 13 बरनूली - प्रमेय : श्यानता15videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.10 प्रत्यास्थता27videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)24videos
सरल रेखा एवं समतल, में कण की गति
Similar Questions
दो पात्रों (vessels) के आधारों के क्षेत्रफल समान है , परंतु आकृतियाँ (shapes) भिन्न - भिन्न है। पहले पात्र के दूसरे पात्र की अपेक्षा किसी ऊँचाई तक भरने पर दो गुना जल आता है क्या दोनों प्रकरणो (cases) के पात्रो के आधारों पर आरोपित बल समान है ?
04:10View Solutionजब हम किसी जल - टोटी (water tap) को अपनी उँगलियों द्वारा बंद करने का प्रयास करते है , तो उँगलियों के बीच की खली जगह से तीव्र जल - धाराएँ फुट निकलती है। व्याख्या करे।
04:06View Solutionदो पदार्थो A और B के लिए प्रतिबल - विकृति (stress-strain) ग्राफ चित्र 1.10-1 में दर्शाए गए है। इन ग्राफो को एक ही पैमाना (scale) मानकर खींचा गया है।
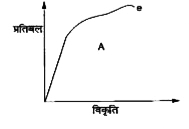
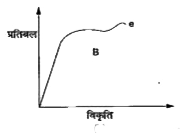
किस पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है ?39:26View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
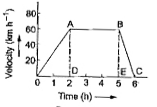 42:43View Solution
42:43View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
50:21View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
51:57View Solutionआवर्ती गति; विस्थापन तथा समय के फलन के रूप में विस्थापन
39:20View Solutionचुम्बकीय क्षेत्र में आवेशित कण की गति
44:11View Solutionचुम्बकीय क्षेत्र में आवेशित कण की गति पर प्रश्न
01:21:02View Solutionचुंबकीय क्षेत्र में आवेशित कण की गति
39:58View Solutionचुम्बकीय क्षेत्र में आवेशित कण की गति
58:30View Solutionचुम्बकीय क्षेत्र में आवेशित कण की गति
01:27:21View Solutionआवेशित कण की चुम्बकीय क्षेत्र में गति
View Solutionसमान E में आवेशित कण की गति
View Solutionचुंबकीय क्षेत्र में आवेशित कण की गति भाग-1
View Solutionएक समान विधुत क्षेत्र में आवेशित कण की गति #!#वृत्ताकार वलय के कारण विधुत क्षेत्र की तीव्रता
View Solution

