किसी धातु के 0.120 kg के गुटके (block) को 100∘C पर गर्म करके, किसी ताँवे के ऊष्मामापी (calorimeter), जिसका द्रव्यमान 100g है और जिसमें 27∘C का 150g जल भरा है, में गिराया जाता है। मिश्रण का अंतिम ताप 32∘C हो जाता है। परिवेश में ऊष्मा क्षय (heat loss) को नगण्य (negligible) मानकर धातु की विशिष्ट ऊष्मा-धारिता परिकलित करें। दिया गया है-जल की विशिष्ट ऊष्मा-धारिता =4186Jkg−1K−1, ताँबे की विशिष्ट ऊष्मा-धारिता =385Jkg−1K−1.
दिया गया है कि
धातु के गुटके का द्रव्यमान m=0.120kg,
ताँबे के ऊष्मामापी का द्रव्यमान mc=100g=0.100kg,
ऊष्मामापी में जल का द्रव्यमान mw=150g=0.15kg,
जल की विशिष्ट ऊष्मा-धारिता cw=4186Jkg−1K−1,
ताँबे की विशिष्ट ऊष्मा-धारिता cc=385Jkg−1K−1,
तप्त गुटके का ताप θ=100∘C∴T=(100+273)K=373K,
ऊष्मामापी और जल का प्रारंभिक ताप θi=27∘C∴Ti=(27+273)K=300k,
मिश्रण का अंतिम ताप θf=32∘C∴Tf=(32+273)k=305K.
धातु के तप्त गुटके द्वारा त्यक्त ऊष्मा =mc(T−Tf), जहाँ c धातु की विशिष्ट ऊष्मा-धारिता है। ऊष्मामापी और इसमें भरे जल द्वारा प्राप्त ऊष्मा
या =mccc(Tf−Ti)+mwcw(Tf−Ti)=(mccc+mwcw)(TfTi).
ऊष्मामापन के सिद्धांत से,
त्यक्त ऊष्मा = प्राप्त ऊष्मा
∴mc(T−Tf)=(mccc+mwcw)(Tf−Ti)
या c=(mccc+mwcw)(Tf−Ti)m(T−Tf)
=(0.1kg×385Jkg−1K−1+0.15kg×4186Jkg−1K−1)(305K−300K)0.120kg(373K−305K)
=(38.5+627.8)×50.120×68Jkg−1K−1
=666.3×58.16Jkg−1K−1
=408Jkg−1K−1.
अतः, धातु की विशिष्ट ऊष्मा-धारिता 408Jkg−1K−1 है।
Topper's Solved these Questions
- ऊष्माBOOK - DAS GUPTACHAPTER - ऊष्माEXERCISE - गेसो का गतिज सिद्धांत
15 Videos
- ऊष्माBOOK - DAS GUPTACHAPTER - ऊष्माEXERCISE - उष्मागतिकी : गैसो की विसिष्ट ऊष्मा-धारिताएँ
12 Videos
- ऊष्माBOOK - DAS GUPTACHAPTER - ऊष्माEXERCISE - ठोसों, द्रव तथा गेसो के प्रसार
9 Videos
- आवेग एवं संवेग : टक्कर BOOK - DAS GUPTACHAPTER - आवेग एवं संवेग : टक्कर EXERCISE - प्रश्नावली (आंकिक प्रश्न)
6 Videos
- ऊष्मा का संचरण BOOK - DAS GUPTACHAPTER - ऊष्मा का संचरण EXERCISE - प्रश्नावली (आंकिक प्रश्न )
13 Videos
Similar Questions
ऑक्सीजन के1X10−3kg द्रव्यमान के लिए PVIT एवं p में, दो अलग-अलग तापों पर ग्राफ दर्शाए गए हैं।
विंदुकित रेखा क्या दर्शाती है?
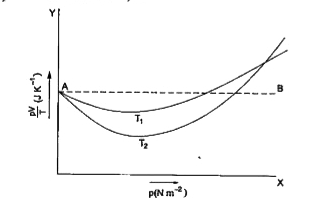
View Solutionकुछ सामान्य गैसों के कमरे के ताप पर मोलर ऊष्मा-धारिताओं के मान नीचे दिए गए हैं

इन गैसों की मापी गई मोलर ऊष्मा-धारिताएँ एकपरमाणुक गैसों की मोलर ऊष्मा-धारिताओं से सुस्पष्ट रूप से भिन्न हैं। प्रतीकात्मक रूप में किसी एकपरमाणुक गैस की मोलर ऊष्मा-धारिता 12.22Jmol−1K−1 होती है। इस अंतर का स्पष्टीकरण कीजिए। क्लोरीन के लिए कुछ अधिक मान (शेष की अपेक्षा) होने से आप क्या निष्कर्ष निकालते हैं?
View Solutionताँबे की चादर में एक वृत्ताकार छिद्र किया गया है। 27∘C पर छिद्र का व्यास 4.24 cm है। इस धातु की चादर को 227∘C तक तप्त करने पर छिद्र के व्यास में क्या परिवर्तन होगा? (ताँबे का रेखीय प्रसार गुणांक =1.78×10−5K−1)
View Solutionयदि किसी पिंड का संवेग 50% से बढ़ता गौ, तो इसकी गतिज ऊर्जा में कितनी वृद्धि होगी ?
View Solutionधातु की एक प्लेट का क्षेत्रफल 595×10−3m2 है और इसकी मोटाई 8.4×10−2m है। इसकी एक सतह का ताप 50∘C और ठीक सामनेवाली दूसरी सतह का ताप 5∘C है। ऊष्मा का वह परिमाण ज्ञात करें जो इसकी एक सतह से दूसरी सतह तक प्रति मिनट प्रवाहित होती है। (धातु की ऊष्मा-चालकता =399Wm−1K−1)
View Solutionमिश्रण का तापमान #!#गुप्त ऊष्मा धारिता #!#अवस्था में परिवर्तन के लिए आवश्यक ऊष्मा
View Solutionतापमान व समय के मध्य ग्राफ #!#ऊष्मा का जल तुल्यांक #!#ऊष्मा धारिता व बर्फ को जमने में लगा समय
View SolutionMgCO3 के 10g को गर्म करने पर, यह 0.1 मोल CO2 और 4gmgO में अपघटित हो जाता है। MgCO3 की प्रतिशत शुद्धता होगी : (दिया गया है, Mg,C और O के परमाणु भार क्रमशः 24,12 और 16 u है)
View Solutionएक धातु ऑक्साइड का सूत्र Z2O3है यह हाइड्रोजन द्वारा अपचयित होकर मुक्त धातु और जल दे सकता है धातु ऑक्साइड 0.1596gके के पूर्ण अपचयन के लिए 6 mg हाइड्रोजन की आवस्यकता होती है धातु का परमाणु भार है
View Solutionस्थिर दाब पर जल की मोलर ऊष्मा धारिता C_(p),75JK^(-1)"mol"^(-1) है । जब 1kg जल को 10kg ऊष्मा दी जाती है जो प्रसार के लिए मुक्त होती है तो तल के ताप में वृद्धि होगी
View Solutionसंगलित अशुद्ध धातु को लकड़ी के हरे रंग के लट्टे के साथ हिलाकर फफोलेदार तांबा को परिष्कृत किया जाता है, क्योंकि इस प्रकार की लकड़ी, हाइड्रोकार्बन गैसों (जैसे CH_4 ) को मुक्त करती है। इस प्रक्रम X को ________ कहा जाता है और इसका उपयोग धातु में प्रारंभ में उपस्थित Y की अशुद्धियों के शुद्धिकरण के लिए किया जाता है। Y _______ है।
View Solutionकिसी विशिष्ट ताप पर जल के 100g में, विद्युत्-अनपघट्य के 5g के विलयन का वाष्प दाब 2985N//m^2 है। शुद्ध जल का वाष्प दाब 3000N//m^2 है। विलेय का अणुभार है:
View Solutionएक गैस 3 atm के स्थिर दाब के विरुद्ध 3 dm^(3) से 5 dm^(3) तक प्रसारित होती है। प्रसार के समय किए गए कार्य का उपयोग 290 K ताप पर 10 मोल जल को गर्म करने के लिए किया जाता है। जल के अंतिम ताप की गणना कीजिए। जल की विशिष्ट ऊष्मा = 4.184 J/ g/K [दिया गया है: 1 atm = 101.33 J]
View Solutionकिसी धातु के टुकड़े के एक सिरे को गर्म करने पर दूसरा सिरा गर्म हो जाता है क्योंकि:
View Solutionउपयुक्त अपचायक के साथ धातु ऑक्साइड को गर्म करके धातु निष्कर्षण की प्रक्रिया को कहा जाता है-
View Solutionएक प्रबल क्षार और एक प्रबल अम्ल के उदासीनीकरण की ऊष्मा 13 .7 kcal है । जब 0 .6 मोल HCI विलयन को NaOH के 0 .25 मोल में मिलाया जाता है, तो मुक्त ऊष्मा है -
View Solution
